冰川物质平衡线的估算方法
【类型】期刊
【作者】崔航,王杰(兰州大学西部环境教育部重点实验室)
【作者单位】兰州大学西部环境教育部重点实验室
【刊名】冰川冻土
【关键词】 冰川;物质平衡;ELA;估算方法
【资助项】国家自然科学基金项目 (41171063);冰冻圈科学国家重点实验室开放基金项目 (SKLCS 2011-03);国家杰出青年科学基金项目 (40925001)
【ISSN号】1000-0240
【页码】P345-354
【年份】2019
【期号】第2期
【期刊卷】1;|7;|8;|2
【摘要】冰川物质平衡线高度(ELA)与气候变化,特别是与气温和降水的变化关系密切,是重建古气候和反映冰川积累和消融变化的重要代用指标.直接观测方法可以获得较为精准的ELA,但不能大范围展开.因此,ELA的间接估算方法,如赫斯法(Hess)、积累区面积比率法(AAR)、面积–高程平衡率法(AABR)、末端至冰斗后壁比率法(THAR)、终碛到最高峰高差比率法(TSAM)、侧碛最大高度法(MELM)、冰斗底部高程法(CF)、冰川作用阈值法(GT)等,得到了广泛的发展与应用.然而,由于受到雪崩或风吹雪补给、表碛覆盖、冰川类型和形态等因素的影响,单一使用某种方法易受到算法本身的限制,误差较大,需综合考虑各种算法的适用性和选取参数的差异,以提高计算的精度,同时也要考虑到后期构造抬升等的影响.
【全文】 文献传递
冰川物质平衡线的估算方法
摘 要:冰川物质平衡线高度(ELA)与气候变化,特别是与气温和降水的变化关系密切,是重建古气候和反映冰川积累和消融变化的重要代用指标.直接观测方法可以获得较为精准的ELA,但不能大范围展开.因此,ELA的间接估算方法,如赫斯法(Hess)、积累区面积比率法(AAR)、面积–高程平衡率法(AABR)、末端至冰斗后壁比率法(THAR)、终碛到最高峰高差比率法(TSAM)、侧碛最大高度法(MELM)、冰斗底部高程法(CF)、冰川作用阈值法(GT)等,得到了广泛的发展与应用.然而,由于受到雪崩或风吹雪补给、表碛覆盖、冰川类型和形态等因素的影响,单一使用某种方法易受到算法本身的限制,误差较大,需综合考虑各种算法的适用性和选取参数的差异,以提高计算的精度,同时也要考虑到后期构造抬升等的影响.
关键词:冰川;物质平衡;ELA;估算方法
0 引言
冰川物质平衡线高度(equilibrium line altitude,ELA),指在非遮阴的平面上,一个平衡年内冰川物质的积累量和消融量正好相等点连线的海拔高度(或附加冰带下限的海拔高度)[1-2],是冰川积累区和消融区分界线的海拔;而雪线(snow line)是湿雪带与附加冰带之间的界限(或附加冰带的上限)[3],又称粒雪线(firn line).大陆型和极大陆型冰川上,雪线附近存在附加冰带,因而雪线位置要高于ELA.而海洋型冰川通常无附加冰带,故雪线与ELA位置重合[1].早在1958年,崔之久[4]在《贡嘎山现代冰川的初步观察》一文中首先使用了雪线的概念,然而该雪线与前文提及的雪线并非等同,是当作ELA的同义语.直到20世纪80年代,这一术语仍然在我国广泛使用,如见诸于《中国冰川概论》[5]和《西藏冰川》[6]等专著中.之后,黄茂桓[7]建议采用国际通用的定义,便于学术交流和使用国内外冰川资料,目前已被大多数学者采用,如王宁练[8]引入灰色关联分析探讨影响冰川ELA变化的主导气候因子,谢自楚等[9]论证了处于稳定状态时冰川ELA处的比净平衡大致等于整个冰川的平均净平衡.
冰川的ELA对气候变化十分敏感,尤其是与固态降水和大气温度间存在密切的相关性.因此,ELA的波动是冰川响应气候变化的一个重要的指标,也可用于重建古气候和预测未来的冰川变化[10].已有许多学者使用统计和分析方法,建立起了ELA处降水和温度之间的关系[11-14],当时冰川ELA处的气温(降水)值可为降水(气温)的确定提供重要依据[2].此外,古ELA的变化值也为较长尺度的区域气候信息对比提供了可能[15].
近年来,国内对冰川面积、长度、物质平衡等的研究关注较多[16-20],而对ELA的研究则相对较少,且有ELA观测的冰川条数较少、序列也较短[21].因此,ELA的观测及其估算方法就显得尤为重要.获得较为精准的ELA有两种方法:1)物质平衡观测所得到的年净平衡为零的位置便是该年度准确的ELA;2)临时考察中,可利用构造法确定ELA,即沿冰川主轴线自上而下挖浅雪坑,观测雪-粒雪-冰的结构,有污化面代表消融区;含有气泡的呈乳白色的附加冰代表进入ELA附近;多层附加冰与强污化面的位置为ELA[22].然而,直接观测方法只能适用于现代冰川,且不能大范围展开;另外,典型冰川的ELA变化是否具有普遍意义,能否代表整个区域的变化趋势也不得而知.因此,ELA的间接估算方法,如赫斯法(Hess)、积累区面积比率法(accumulation area ratio,AAR)、面积-高 程 平 衡 率 法 (area altitude balance ratio,AABR)、末端至冰斗后壁比率法(toe-to-headwall altitude ratio,THAR)、终碛到最高峰高差比率法(terminal to summit altitude method,TSAM)、侧碛最大高度法(maximum elevation of lateral moraines,MELM)、冰斗底部高程法(cirque-floor altitudes,CF)、冰川作用阈值法(glaciation threshold,GT)等就应运而生[2,10].但每种方法都各有其优点和局限性,尤其是由于冰川形态、雪崩和表碛覆盖等对山地冰川物质平衡的复杂影响,任意使用其中的一种方法可能会获得不精确甚至是错误的结果.本文对这些ELA间接算法的基本原理、应用、适用性以及精确程度进行了系统的总结分析和对比.
1 冰川物质平衡线高度(ELA)估算方法
1.1 赫斯法(Hess)
根据冰川流动的原理,积累区冰川的流动矢量(submergence velocity)向下,消融区流动矢量(emergence velocity)向上.因此,积累区冰川的表面形态是向下凹的,而消融区则是向上凸的,即为Hess法的原理.两种形态都能在大比例尺现代冰川地形图的等高线上清楚地表现出来,而二者中间则是等高线比较平直的地带即为平衡线所在位置.该方法的主要问题是如何找到比较平直的等高线,因为某些冰川地形图上等高线表现的不很清晰,尤其是对于规模较小的冰川,导致该方法的精度在一定程度上取决于测量者的冰川野外考察经验[1].
1.2 积累区面积比率法(AAR)
AAR(accumulation area ratio)法是假定冰川处于稳定状态时,冰川积累区的面积占据整个冰川面积的某个固定比例,该比率就是AAR值(图1).AAR法普遍用于重建古冰川和计算现代冰川的ELA,是由 Meier[23]首先提出的.
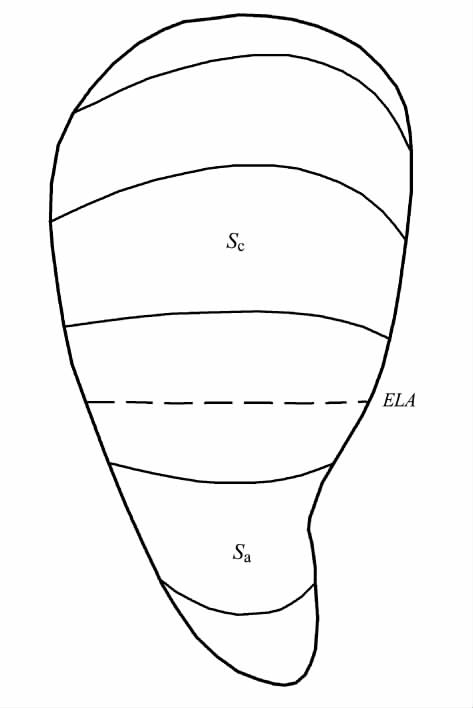
图1 AAR法示意图[23]
注:Sa和Sc分别为冰川消融区和积累区的面积,AAR=Sc/(Sc+Sa)
Fig.1 Schematic diagram of AARmethod[23]
研究表明冰川处于稳定状态时,其AAR在不同的纬度具有不同的值,中高纬度冰川的AAR值介于0.5~0.8[24]或0.55~0.65之间[25],低纬度地区的AAR趋向于一个更高的值(0.8)[26].不同类型的冰川也具有不同的AAR值,对于山谷冰川和冰斗冰川而言,AAR值取0.6±0.05能得到较好的结果[25],而山麓冰川和冰盖由于其面积高程分布的不对称,与山谷和冰斗冰川的AAR值有很大差异[24].冰川末端有表碛覆盖的冰川,由于表碛的隔热作用(相当于增加了冰川消融区的面积),其AAR值普遍偏低(0.4)[26].AAR 值还易受冰川形态特征及其下伏地形的影响[27-28],如果其下伏地形坡度或本身形态特征发生变化,即使是同一冰川,其AAR值也随之改变.
当AAR取值介于0.5~0.8之间时,所得到的ELA可相差上百米[27],因此如何选取最适宜的AAR值是该方法首先需要解决的问题.一些学者致力于求取整个流域冰川的最适宜AAR值,Gross等[29]对阿尔卑斯山脉冰川ELA的区域分析表明,AAR=0.67是最适合重建ELA的AAR值;Aoki[30]则认为在不考虑冰川类型和规模时,AAR=(0.592±0.067)为最适宜重建古ELA的AAR值.Kern等[31]通过对全球冰川AAR值的计算分析发现,AAR值与冰川面积呈现对数相关(AAR=0.0648×lnS+0.483),认为AAR=(0.44±0.07)时较适用于面积在0.1~1km2的冰川,AAR=(0.54±0.07)时适用于面积在1~4km2的冰川,AAR=(0.64±0.04)时适用于面积>4km2的冰川.因此,一旦确定了某个冰川的面积,便可根据这一公式得出适用的AAR值,进而进行ELA的计算.
应用AAR法计算古ELA时,Porter[32]认为需要确定冰川的总面积及冰川表面的等高线: 首先,可以通过侧碛和终碛等冰川作用遗迹来恢复冰川作用的范围,进而确定冰川的总面积;之后,使用THAR、CF和MELM等方法得到一个先验的ELA,再根据Hess法的原理可以绘制出冰川表面的等高线图(图1);最后,计算每两条连续的等高线间冰川的面积,得到冰川面积随高程变化的面积累积曲线,根据这一曲线便可求得与AAR值相对应的 ELA(图2).而 Kaser等[26]认为,在使用AAR法时可以直接使用现代U形谷底部的面积,并非是重建的冰川表面面积,进而得到冰川的面积累计曲线,可以有效的避免重建冰川表面时造成的误差.
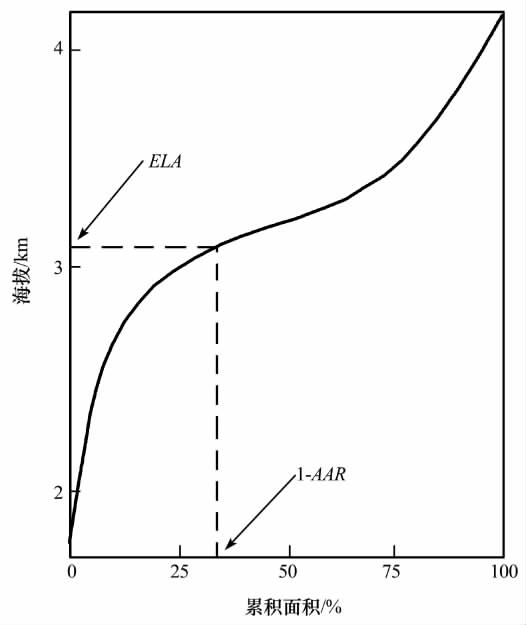
图2 冰川的累计面积(1-AAR对应的高程为ELA)曲线[32]
Fig.2 The cumulative glacierized area(1-AAR)curve,from which the ELA can be determined for a known AAR[32]
AAR法很少考虑冰川形状的变化,尤其是冰川的面积-高程信息.如一个拥有宽的积累区、窄的消融区的冰川与另一个拥有窄的积累区、宽的消融区的冰川,即使二者的ELA相等,也会有不同的AAR值[33].因此,在使用AAR法计算ELA时,应充分考虑所在区域冰川形状、类型和规模等特征,以便得到更为精准的AAR值.
1.3 面积-高程平衡率法(AABR)
AABR(area altitude balance ratio)法利用冰川消融区和积累区物质平衡梯度(物质平衡各分量随高度的变化)的比值,即BR值来计算ELA.它由Furbish等[34]提出,基于以下3点假设:1)冰川积累区和消融区的物质平衡随高度的变化(净物质平衡曲线)都是线性或近似线性的;2)净物质平衡曲线反映的是冰川的一个平衡状态;3)山谷地形充分地限制了冰川,冰川物质平衡改变(从某稳定状态到另一稳定状态)时仅表现为冰川末端的进退变化,即线性的物质平衡曲线能够解释积累区与消融区冰川横剖面的变化,尤其是表面高程的改变.
该方法需要一个确定的BR值,Furbish等[34]提出可以用关系式表示为:
式中:ab、ac分别为消融区与积累区;bn为物质平衡梯度;A为面积;¯z为面积加权平均高度.Aab和Aac可以通过量算得出,¯z可以通过式(2)和(3)求得:
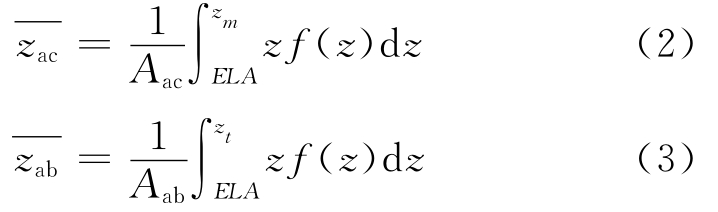
式中:f(z)可由冰川的面积–高程曲线F(z)求导获得(图3);zm和zt分别为冰川最高和末端高程(zab和zab都取正值).通常情况下,由式(2)和(3)计算zab和zab是最为精准的方法(其精度取决于面积–高程曲线拟合线的质量);同时为了提高精度,对非常不规则的面积-高程曲线,需要分别对积累和消融区进行拟合[35].然而,该算法繁琐且非常耗时,不适宜进行大规模的计算;实际应用中,式(4)是计算zab和zab的更为简便可行的方法,只要减小等高线的间距就可有效提高其精度.
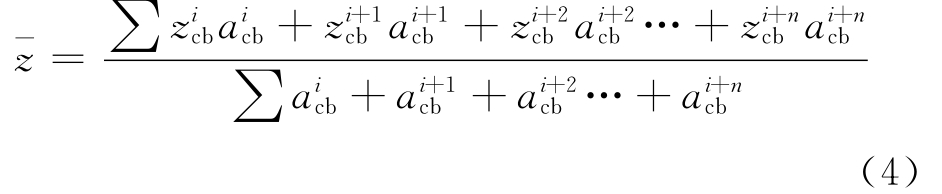
式中: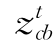 代表两条相邻的等高线的平均高程;acb为对应等高线间的面积.另外,该方法易于在电子表格中进行运算,可以用于多条冰川ELA的同时批量处理[35].
代表两条相邻的等高线的平均高程;acb为对应等高线间的面积.另外,该方法易于在电子表格中进行运算,可以用于多条冰川ELA的同时批量处理[35].
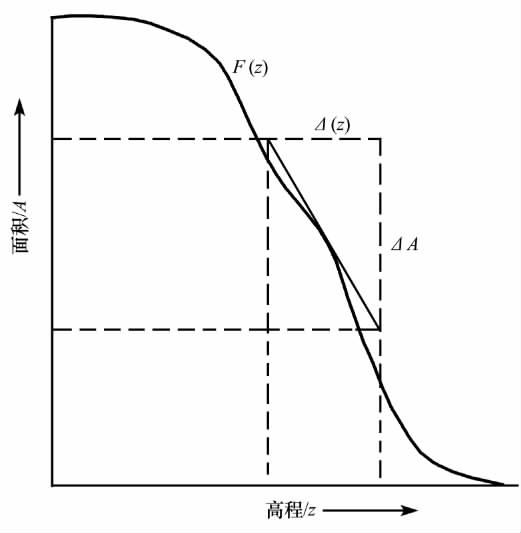
图3 冰川面积–高程曲线F(z)[34]
Fig.3 Hypsometric curve F(z)relating the distribution of glacierized area Ato elevation z[34]
AABR法在计算ELA时首先需要假定一个ELA(如冰川最高与最低点平均海拔高度),划分出冰川的积累与消融区,再根据其面积–高程曲线计算![]() 和Aac的值,随后检测bnab/bnac(即BR值)是否与
和Aac的值,随后检测bnab/bnac(即BR值)是否与![]() 相等.若相等,说明此ELA即为所求的ELA;否则,增加或降低ELA直至bnab/bnac
相等.若相等,说明此ELA即为所求的ELA;否则,增加或降低ELA直至bnab/bnac![]() 的值一致.
的值一致.
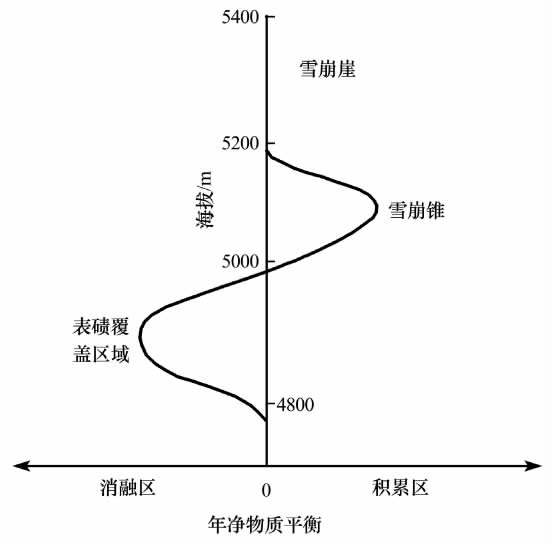
图4 尼泊尔Ama Dablam冰川的物质平衡曲线[10]
Fig.4 Generalised mass-balance curve of the Ama Dablam Glacier,Nepal[10]
1997年,Benn等[33]首先设计了一个用AABR法计算ELA的电子表格,使其所有运算过程都能在计算机上完成.但研究发现,该程序易产生系统误差,进而可能导致略微高估ELA;鉴于此,Osmaston[36]提出了一个改进的算法,进一步提高了AABR法的实用性.
AABR法既能计算现代冰川又能重建古冰川的ELA,较适用于处于平衡状态、物质平衡梯度为线性或接近线性的冰川.雪崩补给占较大比重或表碛覆盖较显著的冰川(图4),其物质平衡曲线不是线性的,AABR法在这些地区并不适用.因而,Benn等[10]提议可以对上述地区冰川的积累区和消融区进行可靠的参数化,使其满足AABR法的先决条件.
1.4 末端至冰斗后壁比率法(THAR)
THAR(toe-to-headwall altitude ratio)法是基于ELA必处于冰川最高点与最低点之间的某个高度处这一事实,其中,THAR值为ELA与冰川最低点高程之差和冰川最高点与最低点高程之差的比值[37](图5),常用于估算古冰川和现代冰川的ELA.Manley[38]认为冰川末端到最高点之间高程的平均值为ELA(THAR=0.5),研究现代冰川时常用这种方法计算ELA[39],也被称为中值高度法(the Median Elevation of Glaciers,MEG).随后,Meierding[40]在计算科罗拉多冰川的ELA时使用的THAR值介于0.35~0.40之间,Murray等[41]证明这一范围非常适用于小型冰斗冰川.Osmaston[42-43]发现低纬山麓冰川和小冰帽最适宜的THAR值分别为0.5和0.3.Porter等[44]认为无表碛覆盖的冰川THAR值通常介于0.4~0.5;而Clark等[45]对美国加利福尼亚州表碛覆盖型冰川的研究发现,由于表碛对冰川消融的影响,该类冰川具有更高的THAR值(0.6~0.8).另外,研究表明阿拉斯加拥有宽积累区和窄消融区冰川的THAR值为0.66[46].
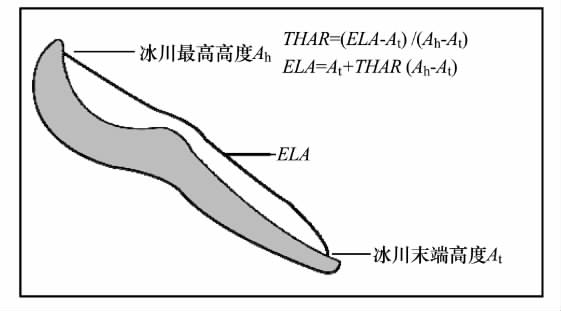
图5 THAR法算法示意图[32]
Fig.5 A schematic diagram of THARmethod[32]
THAR法没有考虑冰川的形状或不同谷地的面积–高程变化,且其值的选择是基于区域的气候状况及冰川特征,是带有较强主观性的选择,而不是根据每条冰川的具体特征[47].此外,雪崩补给对冰川积累影响较大以及冰川的最高点难以确定的区域,这一方法并不适用[10].
计算ELA时用不同的THAR值得到的结果差异很大,因此,确定适宜的THAR值就变得十分重要.Kaser等[26]在研究东非的鲁文佐里山(Ruwenzori Range)冰川时提出了一个图解的方法来确定最适的THAR值:首先,以冰川末端高程为横坐标,以冰川最高点高程为纵坐标建立坐标系,并将此地的冰川分为3组标绘在坐标系中;再将这3组数据分别线性拟合,直线的斜率即为(1-1/THAR),从而计算得出它们的THAR值分别为0.46、0.50和0.57,且这3条直线与经过原点的斜率为1的直线的交点为每组冰川的ELA(图6).通过与该区域AAR法和AABR法重建的ELA的对比发现,该方法估算出的ELA与其他值相差无几.
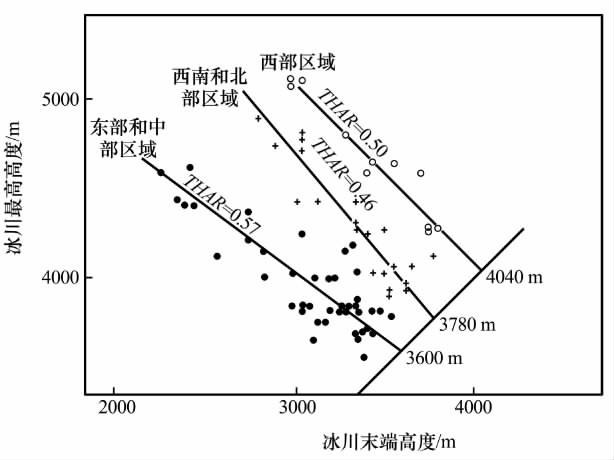
图6 鲁文佐里山末次冰盛期(LGM)75条冰川的THAR算法示意图[26]
Fig.6 Graphically estimating the ELA of 75LGM glaciers on the Rwenzori into three groups by using THAR method[26]
1.5 终碛到最高峰高差比率法(TSAM)
Louis[48]提出可以用流域内最高峰的高程作为冰川的后缘高度,然后利用冰川流域最高峰与终碛垄之间的平均高度算出ELA,即为TSAM(terminal to summit altitude method)法.该方法与THAR法类似,但解决了THAR法冰川后缘高度难以确定的问题[2].Gross等[29]在研究欧洲阿尔卑斯山的冰川时发现,这种方法得出的ELA比实际值高出约100m;而Lehmkuhl[49]在研究蒙古阿尔泰山最北缘的现代冰川时发现,该方法计算出的ELA与野外观测和从航空相片上判读的值吻合较好.与THAR法类似,TSAM法能够快速的计算出ELA,尤其是对于地形图难以获得或不可靠的地区.然而,当整个冰川流域的最高峰不具有代表性且其对冰川的积累贡献很少时,应用TSAM法就会遇到一些问题[10].另外,该方法还有一个难以克服的问题,古冰川多次作用的后缘显然不在同一高度上,也会导致ELA的计算不够准确[2].
更早有一种方法与TSAM法类似,只是用分水岭平均高度(粒雪盆周围的最高峰及鞍部高度平均值)代替最高峰的高程,称为Höfer法[50].该方法在早期的文献中得到了较为广泛的应用,较适合于计算规模较小的冰斗和山谷冰川.但即使针对同一条冰川,不同学者选取的最高峰或鞍部的值都会有所差异,进而计算出不同的ELA[10].
1.6 侧碛最大高度法(MELM)
Lichtenecker[51]提 出 侧 碛 的 最 大 高 度 (maximum elevation of lateral moraines,MELM)法可以近似地代表ELA,因为冰川在积累区向中心而消融区向边缘流动,且净消融只发生在消融区,因此理论上仅在ELA之下才发生边缘冰碛的沉积(图7),导致ELA的高度一定在侧碛最大高度之上[52-53].
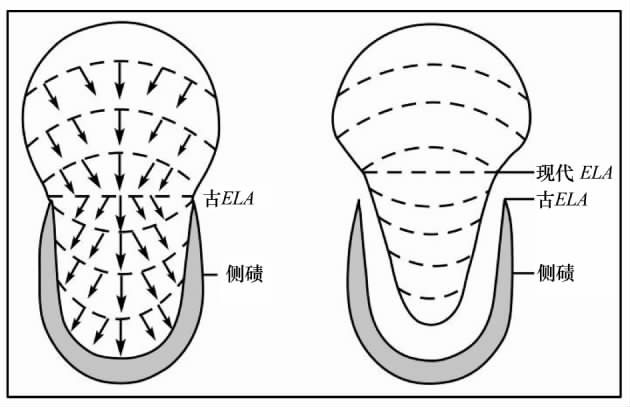
图7 MELM法示意图[28]
Fig.7 Schematic diagram of the MELM method[28]
然而,用MELM法重建ELA时会遇到一些问题[10,54]:1)ELA以下随着冰川消融,冰川内碛可能不会立刻达到冰川表面,这意味着侧碛开始形成的位置在ELA以下,此时MELM法重建的ELA偏低;2)冰消期时侵蚀作用或地形(坡度太陡峭而不利于侧碛的积累)的影响,导致会极大低估ELA;3)当冰川为冰帽或冰盖时,冰碛物有时部分或完全围绕冰体分布并堆积于冰川的前面而不是侧面,侧碛最大高度会低于ELA;4)冰川退缩非常缓慢时,冰碛物会沿着早期形成的侧碛向上游方向不断堆积,从而导致高估ELA.
虽然存在这些不确定因素,但对表碛覆盖型且难以获得物质平衡梯度形态的古冰川,侧碛保存又相对完好,MELM方法能提供最真实可靠的ELA;此外,该方法不需要详细的地形资料,可以通过航空相片或野外测量直接获得[10].Porter[32]和 Benn等[54]认为,通常情况下,MELM法取得的高度为ELA的最小值,根据这一阈值可以筛选其他方法计算出的ELA(只取大于该阈值的ELA),从而提高计算的精度.
1.7 冰斗底部高程法(CF)
CF(cirque-floor altitudes)法认为冰斗底部高程对古ELA有很重要的指示作用,可近似等同于ELA[40].然而,冰斗底部高程与ELA之间未必有必然的联系[10],如当冰川为冰斗冰川时,ELA要略高于冰斗底部的高程;而当冰川为山谷冰川时,ELA将低于(甚至是远低于)冰斗底部高程[32](图8).Hamann等[55]发现,在奥地利阿尔卑斯山区,冰斗底部高程强烈地受到以前地形的影响,特别是第三纪剥蚀面的位置.另外,冰斗经受多次冰期旋回后,很难将它归属于某一个特定的冰川作用时期,也限制了它作为古气候重建指标的应用[10].虽然有这些因素限制,但它对冰川作用水准面的区域趋势和长尺度的平均气候状况仍有很重要的指示作用[56].
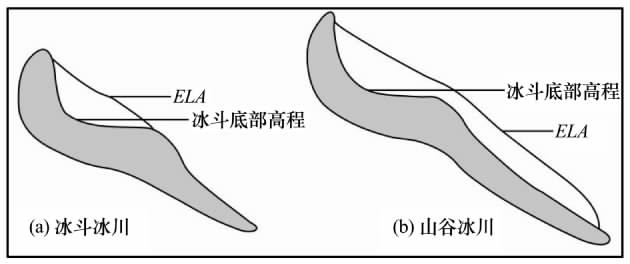
图8 ELA与冰斗底部关系示意图[32]
Fig.8 The relationship between ELA and cirque-floor[32]
1.8 冰川作用阈值法(GT)
GT(glaciation threshold)法是某一区域内,同时代的有冰川发育的最低山头与无冰川发育的最高山头间平均高度,常被用来确定区域的ELA[41,51-52].虽 然 GT 可 以 代 表 区 域 ELA 的 趋势,但其通常要比实际ELA高100~200m[40];另外,用GT法计算ELA时,需要确定并标绘出该时段这一区域全部有冰川作用和无冰川作用的山峰[32],且要排除太陡的山峰(不发育冰川,但其高度会超过有冰川发育的山头的高度),如此大量的野外工作在实际应用中通常是不现实的.用于重建古ELA时最困难的是确定哪些是同时期的有冰川作用和无冰川作用的山峰[47].
2 额外潜在的误差来源
2.1 构造运动
古冰川ELA的重建,必须要考虑研究区冰期后构造运动的影响[39,57-58],因为它会改变冰期后当地的气候状况(温度和降水等)以及古ELA的准确位置,尤其是在地表升、降速率较大的构造活动强烈的地区这种影响更大.构造沉降地区,古ELA的真实值是用各种方法重建出的ELA与下沉量之和,而构造抬升地区则是重建的ELA与抬升量之差.
2.2 冰期海平面变化
冰期时海平面高度的下降是否影响古冰川ELA的重建还存在一定争议.Broecker[59]和Porter[60]认为由于末次冰期时海平面高度比现今低至少120m,重建古ELA尤其是据ELA差值(ΔELA)推算温度的变化状况时,应进行相应的校正;因为冰期时ELA比之重建的ELA海拔更高(相对海平面),相应的温度也更低,从而直接用ΔELA推算的温度变化量就包含了海平面降低导致的海拔效应,实际运用中ΔELA应扣除海平面的下降值(SLm-SLg)(图9).然而,由于各地冰期并不一定同步,很难知晓ELA降低时海平面下降的确切值,因此,基于此进行的校正只能带入更大的误差[61].同时 Benn等[54]和 Osmaston[61]发现,即使冰期时海平面下降,在给定高度处的温度也不会发生很大变化.这是由于海平面下降而空出的体积与增加的冰川体积大致相当,对流层未发生整体的上升或下降.因此,任意高度上部的大气质量没有发生变化,此时假定两种状况:1)气候稳定时,该高度处温度是不变的,但由于更高的大气压力和绝热升温,降低的海平面的温度是升高的;2)气候变冷时,由于海洋的收缩,大气层将更靠近地球中心,温度将发生几乎可以忽略的轻微变化;但气候的变冷,也会导致整个大气层的收缩,进而导致更高的垂直递减率和同一高度处温度的降低,尽管这种效应很显著,但它是随时间和空间而变化的,也没有理由认为应该校正ELA.另外,Hebenstreit[15]认为ELA的值是地形与大气相互作用的结果,因此海平面的降低并不能改变与大气相关的ELA的真实值.
表1 乌鲁木齐河源LGM时ELA的估算结果[62]
Table 1 The calculated ELAs at the headwaters of theÜrümqi River during LGM[62]

注:*当BR值取3.5时,相应的ELA低于MELM法获得的ELA最小阈值,因此将其舍弃.
平均参数值 0.55 0.65 0.5 3550 1.0 1.5 2.0 2.5 3.0 3.5*方法 AAR THAR MELM AABR ELA/m 3615 3675 3690 3550 3667 3625 3595 3571 3552 3535 3616
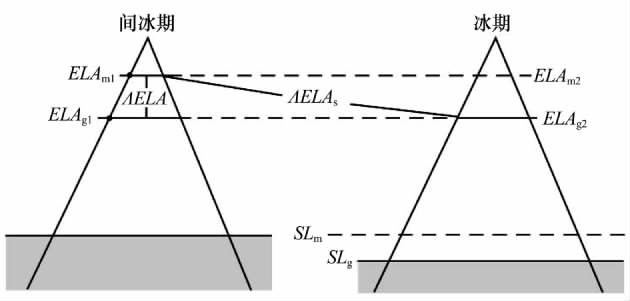
图9 冰期–间冰期海平面变化对ΔELA的影响[32]
注:SLm和SLg分别为间冰期和冰期的海平面高度;ELAm1和ELAg1分别为相对于SLm的间冰期和冰期的ELA,ELAm2和ELAg2为相对于SLg的间冰期和冰期的ELA,ΔELAs=ΔELA-(SLm-SLg)
Fig.9 The effect of sea level changes onΔELA during the glacial-interglacial cycle[32]
3 讨论
Hess法仅适用于有地形图绘制的冰川作用区,这极大地限制了其在古冰川ELA估算中的应用.CF、MELM和GT法,在海洋型冰川作用等侵蚀较强烈的区域,冰川地形常保存不完整,致使其估算的误差较大.此外,由于海洋型冰川几乎在整个平衡年内消融都较强[33],故仅需较小的消融区就能使冰川保持平衡,其往往拥有较大的AAR和BR值;且与极大陆型和大陆型冰川相比,海洋型冰川的ELA更接近于冰川末端,THAR值一般较小.
没有哪一种ELA的估算方法是适用于所有情况,因此选取方法时,需综合考虑研究区冰川的类型、流域的地形和气候环境条件.条件允许的情况下,应尽可能使用多种方法,并评估每种算法的可靠性,对比分析各算法得出的ELA的差异,从而获得最理想的ELA.Xu等[62]应用多种估算ELA的方法重建天山乌鲁木齐河源LGM时的ELA(表1),发现当AAR值取0.55和0.65时,所得的ELA相差60m,其中,0.55为乌鲁木齐河源1号冰川多年观测的均值,0.65为统计得出的处于稳定状态冰川的AAR值.显然,当AAR取0.55时相应的ELA与平均值更接近,因此,以现代冰川的参数为依据进行反推更为有效.AAR法较之THAR法和MELM法,其获得的ELA(均值为海拔3645m)与平均值更接近,后两者精度虽低,但可为AAR与AABR法提供依据;AABR法获得的ELA(均值为海拔3602m)与平均值最为接近;即便如此,仅用某一BR值计算,也可能会导致较差甚至错误的结果.因此,单一方法获得的ELA易受方法自身的限制,而多种方法估算的平均值能有效地减小算法本身可能产生的和部分偶然的误差.
4 结论
(1)Hess法的精度取决于绘制的冰川地形图的精度以及判读人的冰川学知识,且受地形图绘制时间的限制,只能计算地形图绘制时的ELA,而不能实时地反映ELA的变化.
(2)AAR法涵盖有通常形态冰川的物质平衡和面积-高程信息,与THAR、MELM、TSAM、CF、GT等方法相比,其精度较高;而比之AABR法,计算更简便,且几乎适用于所有类型的冰川,但精确度稍差,应用时需充分考虑研究区冰川的特征(形状、规模与类型等),以选取最适宜的值.
(3)AABR法既兼顾了冰川的面积-高程信息也考虑了具体的物质平衡梯度,是较为精准的ELA算法,但其较适用于物质平衡梯度为线性或接近线性的,如非雪崩补给且无表碛或表碛覆盖较少的冰川和冰帽,也需要详细且精确的地貌图和地形图(或航空相片),这使其难以应用于所有类型的冰川.
(4)THAR、TSAM和CF法基于冰川作用流域的总体形态估算ELA,能快速获得结果,较适用于详细地图资料缺乏的地区;但未考虑冰川的物质平衡,且与冰川实际的ELA未必有必然的联系,致使其精度偏低,估算出的ELA通常被认为仅是ELA的近似值,只能为其他更精准方法(AAR法或AABR法)的估算提供参考.
(5)MELM法利用了冰川物质平衡和冰川沉积模式的关系,认为侧碛的最大高度近似代表冰川的ELA,不需要详细的重建古冰川的表面形态,较适用于缺少地形图资料、侧碛保存较好的冰川作用区.
(6)GT能代表区域ELA的趋势,便于进行区域间的对比,但其需要大量的野外工作,且易受地形限制.
参考文献(
References):
[1]Xie Zichu,Liu Chaohai.Introduction of Glaciology [M].Shanghai:Shanghai Popular Science Press,2010:116-124.[谢自楚,刘潮海.冰川学导论[M].上海:上海科学普及出版社,2010:116-124.]
[2]Ju Yuanjiang,Liu Gengnian,Zhang Xiaoyong,et al.High mountain glaciers’ELA0and climate[J].Progress in Geography,2004,23(3):43-49.[鞠远江,刘耕年,张晓咏,等.山地冰川物质平衡线与气候[J].地理科学进展,2004,23(3):43-49.]
[3]Paterson W S B.The Physics of Glaciers[M].3rd Edition.Oxford,UK:Pergarnon Press,1994:8-25.
[4]Cui Zhijiu.A primary study of the modern glacier of Gongga Mountain[J].Acta Geographica Sinica,1958,24(3):318–342.[崔之久.贡嘎山现代冰川的初步观察[J].地理学报,1958,24(3):318-342.]
[5]Shi Yafeng,Huang Maohuan,Ren Binghui.An Introduction to the Glaciers in China[M].Beijing:Science Press,1988.[施雅风,黄茂桓,任炳辉.中国冰川概论[M].北京:科学出版社,1988.]
[6]Li Jijun,Zheng Benxing,Yang Xijin,et al.Glaciers of Xizang(Tibet)[M].Beijing:Science Press,1986.[李吉均,郑本兴,杨锡金,等.西藏冰川[M].北京:科学出版社,1986.]
[7]Huang Maohuan.The snowline/the Equilibrium line[J].Journal of Glaciology and Geocryology,1992,14(3):285-286.[黄茂桓.雪线、平衡线[J].冰川冻土,1992,14(3):285-286.]
[8]Wang Ninglian.Grey relational analysis of the leading climatic factor influencing the changes of the equilibrium line[J].Journal of Glaciology and Geocryology,1995,17(1):8-15.[王宁练.冰川平衡线变化的主导气候因子灰色关联分析[J].冰川冻土,1995,17(1):8-15.]
[9]Xie Zichu,Ding Liangfu,Liu Chaohai,et al.Mass balance at the steady state equilibrium line altitude and its application[J].Journal of Glaciology and Geocryology,1996,18(1):1-9.[谢自楚,丁良福,刘潮海,等.冰川零平衡线处的物质平衡及其应用[J].冰川冻土,1996,18(1):1-9.]
[10]Benn D I,Lehmkuhl F.Mass balance and equilibrium-line altitudes of glaciers in high-mountain environments[J].Quaternary International,2000,65-66:15-29.
[11]Shi Yafeng,Zheng Benxing,Li Shijie.Last glaciation and maximum glaciation in the Qinghai-Xizang(Tibet)Plateau:A controversy to M.Kuhle's ice sheet hypothesis[J].Chinese Geographical Science,1992,2(4):293-311.
[12]Ohmura A,Kasser P,Funk M.Climate at the equilibrium line of glaciers[J].Journal of Glaciology,1992,38:397-411.
[13]Kuhn M.On the computation of heat transfer coefficients from energy-balance gradients on a glacier[J].Journal of Glaciology,1979,22(87):263-272.
[14]Ambach W.Climatic shift of the equilibrium line:Kuhn's concept applied to the Greenland ice cap[J].Annals of Glaciology,1985,6:76-78.
[15]Hebenstreit R.Present and former equilibrium line altitudes in the Taiwanese high mountain range[J].Quaternary International,2006,147(1):70-75.
[16]Wang Guoya,Shen Yongping.The effect of change in glacierized area on the calculation of mass balance in the Glacier No.1at the headwaters ofÜrümqi River[J].Journal of Glaciology and Geocryology,2011,33(1):1-7.[王国亚,沈永平.天山乌鲁木齐河源1号冰川面积变化对物质平衡计算的影响[J].冰川冻土,2011,33(1):1-7.]
[17]Zhang Guofei,Li Zhongqin,Wang Wenbin,et al.Change processes and characteristics of mass balance of theÜrümqi Glacier No.1at the headwaters of theürümqi River,Tianshan Mountains,during 1959—2009[J].Journal of Glaciology and Geocryology,2012,34(6):1301-1309.[张国飞,李忠勤,王文彬,等.天山乌鲁木齐河源1号冰川1959—2009年物质平衡变化过程及特征研究[J].冰川冻土,2012,34(6):1301-1309.]
[18]Wang Sheng,Pu Jianchen,Wang Ninglian.Study of mass balance and sensibility to climate change of Qiyi Glacier in Qilian Mountains[J].Journal of Glaciology and Geocryology,2011,33(6):1214-1221.[王盛,蒲健辰,王宁练.祁连山七一冰川物质平衡及其对气候变化的敏感性研究[J].冰川冻土,2011,33(6):1214-1221.]
[19]Gao Xin,Zhang Shiqiang,Ye Baisheng,et al.Glacier runoff change in the upper stream of Yarkant River and its impact on river runoff during 1961—2006[J].Journal of Glaciology and Geocryology,2010,32(3):445-453.[高鑫,张世强,叶柏生,等.1961—2006年叶尔羌河上游流域冰川融水变化及其对径流的影响[J].冰川冻土,2010,32(3):445-453.]
[20]Xu Mingxing,Yan Ming,Kang Jiancheng,et al.Comparative studies of the glacier mass-balance and their climatic implications in Svalbard,Scandinavia and southern Norway[J].Journal of Glaciology and Geocryology,2010,32(4):641-649.[徐明星,闫明,康建成,等.北极Svalbard、斯堪的纳维亚与挪威南部冰川物质平衡对比及其气候意义[J].冰川冻土,2010,32(4):641-649.]
[21]Pu Jianchen,Yao Tandong,Yang Meixue,et al.Rapid decrease of mass balance observed in the Xiao(Lesser)Dongkemadi Glacier,in the central Tibetan Plateau[J].Hydrological Processes,2008,22(16):2953-2958.
[22]Liu Shiyin,Liu Chaohai,Xie Zichu,et al.Field Observations in Glaciological Research[M].Beijing:Science Press,2012:46-48.[刘时银,刘潮海,谢自楚,等.冰川观测与研究方法[M].北京:科学出版社,2012:46-48.]
[23]Meier M F.Proposed definitions for glacier mass budget terms[J].Journal of Glaciology,1962,4(33):252-263.
[24]Meier M F,Post A S.Recent variations in mass net budgets of glaciers in western North America[C]//Variations of the Re-gime of Existing Glaciers,Symposium of Obergurgl 1962.International Association of Hydrological Sciences Publication,1962,58:63-77.
[25]Porter S T.Equilibrium line altitude of late Quaternary glaciers in the Southern Alps,New Zealand [J].Quaternary Research,1975,5:27-47.
[26]Kaser G,Osmaston H.Tropical Glaciers[M].Cambridge,UK:Cambridge University Press,2002:149-192.
[27]Wang Ninglian,Pu Jianchen,Liu Shiyin,et al.Study on AAR of valley glaciers in the steady state[J].Journal of Glaciology and Geocryology,1997,19(2):167-172.[王宁练,蒲健辰,刘时银,等.山谷冰川稳定态时积累区面积比率研究[J].冰川冻土,1997,19(2):167-172.]
[28]Nesje A.Topographical effects on equilibrium-line altitude on glaciers[J].GeoJoural,1992,27(4):383-391.
[29]Gross G,Kerschner H,Patzelt G.Metodische Untersuchungenüber die Schneegrenze in alpinen Gletschergebieten[J].Zeitschrift für Gletscherkunde und Glazialgeologie,1977,12:223-251.(in German)
[30]Aoki T.Evaluation of the accumulation area ratio (AAR)method based on mass balance data for modern glaciers[J].Geographical Review of Japan,1999,72:763-772.
[31]Kern Z,Laszlo P.Size specific steady-state accumulation-area ratio:an improvement for equilibrium-line estimation of small palaeoglaciers[J].Quaternary Science Reviews,2010,29:2781-2787.
[32]Porter S C.Snowline depression in the tropics during the Last Glaciation[J].Quaternary Science Reviews,2001,20:1067-1091.
[33]Benn D I,Gemmell A M D.Calculating equilibrium-line altitudes of former glaciers by the balance ratio method:a new computer spreadsheet[J/OL].Glacial Geology and Geomorphology,1997.
[34]Furbish D J,Andrews J T.The use of hypsometry to indicate long-term stability and respond of valley glaciers to changes in mass transfer[J].Journal of Glaciology,1984,30:199-211.
[35]Rea B R.Defining modern day Area-Altitude Balance Ratios(AABRs)and their use in glacier-climate reconstructions[J].Quaternary Science Research,2009,28:237-248.
[36]Osmaston H.Estimates of glacier equilibrium line altitudes by the Area Altitude,the Area Altitude Balance Ratio and the Area Altitude Balance Index methods and their validation[J].Quaternary International,2005,138-139:22-31.
[37]Torsnes I,Rye N,Nesje A.Modern and Little Ice Age equilibrium-line altitudes on outlet valley glaciers from Jostedalsbreen,western Norway:an evaluation of different approaches to their calculation[J].Arctic and Alpine Research,1993,25(2):106-116.
[38]Manley G.The late-glacial climate of north-west England[J].Geological Journal,1961,2(2):188-215.
[39]Zhang Wei,Yan Ling,Cui Zhijiu,et al.Present and late Pleistocene equilibrium line altitudes in Changbai Shan,Northeast China[J].Quaternary Sciences,2008,28(4):739-745.[张威,闫玲,崔之久,等.长白山现代理论雪线和古雪线高度[J].第四纪研究,2008,28(4):739-745.]
[40]Meierding T C.Late Pleistocene glacial equilibrium-line in the Colorado Front Range:A comparison of methods[J].Quater-nary Research,1982,18(3):289-310.
[41]Murray D R,Locke W W III.Dynamics of the late Pleistocene Big Timber glacier,Crazy Mountains,Montana,U.S.A.[J].Journal of Glaciology,1989,35(120):183-190.
[42]Osmaston,H A.The Past and Present Climate and Vegetation of Ruwenzori and Its Neighborhood[D].Oxford,UK:University of Oxford,1965.
[43]Osmaston H A.Models for the estimation of firnlines of present and Pleistocene glaciers[C]//Processes in Physical and Human Geography:Bristol Essays.London:Heinemann Educational,1975:218-245.
[44]Porter S C,Pierce K L,Hamilton T D.Late Wisconsin mountain glaciation in the western United States[C]//Late-Quaternary Environments of the United States:The Late Pleistocene.Minneapolis, Minnesota: University of Minnesota Press,1983:71-111.
[45]Clark D H,Clark M M,Gillespie A R.Debris-covered glaciers in the Sierra Nevada,California,and their implications for snowline reconstructions[J].Quaternary Research,1994,41:139-153.
[46]Pewe T L,Reger R D.Modern and Wisconsinan snow lines in Alaska[C]//Proceedings of the 24th International Geologic Congress,Section 12,Montreal,Canada,1972:187-197.
[47]Ramge J M,Smith J A,Rodbell D T.Comparing reconstructed Pleistocene equilibrium-line altitudes in the tropical Andes of central Peru[J].Journal of Quaternary Science,2005,20:777-788.
[48]Louis H.Schneegrenze und Schneegrenzbestimmung[C]//Meynen E.Geographisches Taschenbuch 1954/1955.Wiesbaden,Germany:Franz Steiner Verlag,1955:414-418.(in German)
[49]Lehmkuhl F.Quaternary glaciations in central and western Mongolia[J].Quaternary Proceedings,1998,6:153-167.
[50]Höfer von Heimhalt H.Gletscher-und Eiszeitstudien[C]//Sitzungsberichte der Akademie der Wissenschaften in Wien,Mathematisch-Naturwissenschaftliche Klasse, Abteilung I,Biologie,Mineralogie,Erdkunde 79,1879:331-367.(in German)
[51]Lichtenecker N.Die gegenwaK rtige und die eiszeitliche Schneegrenze in den Ostalpen[C]//Goktzinger G.Vethandlungen der III Internationalen Quartar-Conferenz,Vienna,September 1936.Vienna,Austria:INQUA,1938:141-147.(in German)
[52]Andrews J T.Glacial Systems:An Approach to Glaciers and Their Environments[M].North Scituate,Massachusetts:Duxbury Press,1975.
[53]Visser P C.Glaziologie[M]//Wissenschaftliche ergebnisse der Niederla Kndischen Expeditionen in den Karakorum und die angrenzenden gebiete in den jahren 1922,19251929/30und 1935.Leiden,Netherlands:E J Brill,1938:1-227.(in German)
[54]Benn D I,Owen L A,Osmaston H A.Reconstruction of equilibrium-line altitudes for tropical and sub-tropical glaciers[J].Quaternary International,2005,8:138139.
[55]Hamann C,Embleton C.Morphometrische Analyse der Kare in den Salzburger Zentralalpen[J].Salzburger Geographische Arbeiten,1988,17:57-74.
[56]Robinson G,Peterson J A,Anderson P M.Trend surface a-nalysis of Corrie altitudes in Scotland[J].Scottish Geographical Magazine,1971,87(2):142-146.
[57]Benn D I,Evans D J A.Glaciers and Glaciation[M].2nd Edition.London:Hodder Education,2010:22-56.
[58]Porter S C.Glaciation limit in New Zealand's Southern Alps[J].Arctic and Alpine Research,1975,7(1):33-37.
[59]Broecker W S.Mountain glaciers:recorders of atmospheric water vapor content?[J].Global Biogeochemical Cycles,1997,11:589597.
[60]Porter S C.Pleistocene snowlines and glaciation of the Hawaiian Islands[J].Quaternary International,2005,138:118-128.
[61]Osmaston H.Should Quaternary sea-level changes be used to correct glacier ELAs,vegetation belt altitudes and sea level temperatures for inferring climate changes?[J].Quaternary Research,2006,65(2):244-251.
[62]Xu Xiangke,Wang Liqiang,Yang Jianqiang.Last Glacial Maximum climate inferences from integrated reconstruction of glacier equilibrium-line altitude for the head of theÜrümqi River,Tianshan Mountains [J].Quaternary International,2010,218:3-12.
The Methods for Estimating the Equilibrium Line Altitudes of a Glacier
Abstract:There is a very close connection between the equilibrium line altitude(ELA)and the local climate,particularly solid precipitation and air temperatures.Fluctuations in the ELA therefore provide a pronounced indicator of glacier response to climate change,and help to reconstruct the former climates and to predicate the future glacier behavior.For the glaciers at present,direct observation of glacier mass balance over several years is an ideal method to obtain accurate ELA.However,for a greater range,other estimating methods have to employed,e.g.,accumulation area ratio(AAR),area altitude balance ratio(AABR),toe-to-headwall altitude ratio (THAR),terminal to summit altitude method(TSAM),maximum elevation of lateral moraines(MELM),cirque-floor altitudes(CF)and glaciation threshold(GT).Due to the combined influence of avalanches and snow drift,debris cover and topographic effects(glacier morphologies and styles),the ELAs of a glacier estimated with various methods may have discrepancies of several hundred meters.It is necessary to employ multiple methods,together with an appraisal of their reliability.Furthermore,the tectonic uplift should be considered as well.
Key words:glacier;mass balance;equilibrium line altitude;estimating method
中图分类号:P343.6
文献标识码:A
doi:10.7522/j.issn.1000-0240.2013.0041
Cui Hang,Wang Jie.The methods for estimating the equilibrium line altitudes of a glacier[J].Journal of Glaciology and Geocryology,2013,35(2):345-354.[崔航,王杰.冰川物质平衡线的估算方法[J].冰川冻土,2013,35(2):345-354.]
收稿日期:2012-10-29;
修订日期:2013-02-20
基金项目:国家自然科学基金项目(41171063);冰冻圈科学国家重点实验室开放基金项目(SKLCS 2011-03);国家杰出青年科学基金项目(40925001)资助
*通讯作者:王杰,E-mail:wangjie@lzu.edu.cn
