最优代表向量法及其在冰川分类中的应用
【类型】期刊
【作者】曾溢良,张胜(北京科技大学自动化学院)
【作者单位】北京科技大学自动化学院
【刊名】北京理工大学学报
【关键词】 高光谱遥感;图像分类;最优代表向量;密度峰值聚类;冰川分类
【资助项】高分辨率对地观测系统重大专项基金资助项目;“十三五”武器装备预研领域基金资助项目;中央高校基本科研业务费专项资金资助项目(frf-tp-15-117a1);中国博士后科学基金资助项目...
【ISSN号】1001-0645
【页码】P1067-1071
【年份】2019
【期号】第10期
【期刊卷】1;|6;|7;|8;|4;|5;|2
【摘要】针对同物异谱现象以及分类过程中样本代表性差、人工参数设置等原因导致高光谱遥感影像分类精度差的问题,提出了一种样本集优化的最优代表向量分类法,对感兴趣区中的样本进行密度峰值聚类提纯,并对每类地物提纯后样本的均值向量集进行隶属度聚类择优,获取最优代表向量集作为该类地物的中心向量,最终依据距离准则进行分类.通过对比实验验证,本文算法总体分类精度高于90%,表明最优代表向量分类法能够有效消除样本差异性的影响,提高冰川分类精度.
【全文】 文献传递
最优代表向量法及其在冰川分类中的应用
摘 要: 针对同物异谱现象以及分类过程中样本代表性差、人工参数设置等原因导致高光谱遥感影像分类精度差的问题,提出了一种样本集优化的最优代表向量分类法,对感兴趣区中的样本进行密度峰值聚类提纯,并对每类地物提纯后样本的均值向量集进行隶属度聚类择优,获取最优代表向量集作为该类地物的中心向量,最终依据距离准则进行分类. 通过对比实验验证,本文算法总体分类精度高于90%,表明最优代表向量分类法能够有效消除样本差异性的影响,提高冰川分类精度.
关键词: 高光谱遥感;图像分类;最优代表向量;密度峰值聚类;冰川分类
冰川中蕴含着极其丰富的淡水资源,对全球气候变化与生态平衡起着关键性的作用,但大部分冰川地处偏僻,面积宽广,所以遥感技术被广泛应用于大尺度的冰川监测中[1]. 近年来,全球流域冰川监测研究主要采用Landsat ETM+、SPOT5、 ASTER等多光谱遥感影像,而高光谱遥感影像应用较少. 然而,遥感光谱探测器光谱分辨率的不断提高加快了遥感技术的发展,使高光谱遥感成为遥感领域重要的研究方向之一. 高光谱遥感图像包含丰富的光谱信息,不同的地物在不同的波段下有着明显的差异性,提高了地物的分类识别能力,并且在地表分类、目标探测、农业监测、矿物填图等领域能够提供普通遥感图像不具备的详细、精确的信息[2-3]. 由此可见,高光谱遥感图像在冰川监测方面具备很大的利用潜力.
冰川遥感图像分类是冰川监测的主要技术之一. 目前,国内外学者已经进行了深入研究,胥海威等[4]提出了随机决策树群算法,并利用降维后的青海省祁连县Hyperion高光谱影像进行冰川分类,结果表明该算法不需要降维且分类效果最好;李光辉等[5]利用两种降维方式后的“中习一号”冰川机载高光谱数据与多光谱图像进行了6种图像监督分类方法的对比,结果表明高光谱遥感图像经变换后,分别采用马氏距离法与波谱角法分类效果最佳;赵健赟等[6]利用老虎沟冰川的多光谱Landsat TM、DEM等数据,比较了基于多尺度分割的面向对象分类法与基于像元分类法,结果表明前者的总体分类精度比后者提高了2.47%,并且错分率下降了2.5%;Narama等[7]利用Landsat卫星影像TM3/TM5波段组合的比值阈值法对吉尔吉斯斯坦Terskey-Alatoo地区的冰川进行了研究,结果显示该地区冰川面积呈现了退缩的趋势;Gjermundsen等[8]利用ASTER影像对波段比值法、归一化雪盖指数法以及监督分类3种提取冰川信息的方法进行了评估,结果显示波段比值法对于冰川信息的提取效果最好; Raza等[9]利用Landsat TM和ETM+冰川多光谱遥感图像分别进行了基于像素的分类与基于对象的分类,对比结果表明基于对象的分类效果比基于像素分类高出10%.
由此可见,目前的研究主要针对多光谱影像进行冰川提取,而针对高光谱遥感影像冰川提取的研究较少,并且仍存在着阈值设置难、样本代表性差、识别范围相交等问题. 为解决上述问题,本文针对高光谱冰川遥感影像监督分类法,以青藏高原境内冰川的Hyperion高光谱影像为实验数据,在数据降维基础上,利用改进的密度峰值聚类法与隶属度均值聚类法分别对每类地物的样本与代表向量进行优化,实现了对冰川的准确分类.
1 自动子空间划分联合波段选择
高光谱遥感影像提供丰富光谱信息的同时,大量的光谱波段数据也导致了信息冗余和数据处理困难,并且有限的监督分类训练样本也会带来了维数灾难,即所谓的Hughes现象. 因此,本文将通过波段选择的方式进行数据降维处理.
本文通过计算预处理后Hyperion高光谱影像任意两波段的相关系数得到相关系数矩阵,并绘制影像相邻波段相关系数曲线图将所有波段分成几个子空间. 在进行自动子空间划分后,分别根据式(1)计算每个子空间各个波段的波段指数. 选择各个子空间波段指数较大的波段作为最优的波段,其最优波段数目可调.
式中:Si为第i个波段的标准差;Ri-1,1,R1,i+1为第i波段与其前后两波段的相关系数或i波段与任意两个波段的相关系数;Ii为第i个波段指数的大小.
2 分层密度峰值聚类优化
传统监督分类法选择的感兴趣区域中往往含有一些冗余样本,导致每类地物计算的均值向量代表性较差,降低了分类精度. 为减少冗余样本,提高样本的代表性,本文在密度峰值聚类法[10](CFSFDP)的基础上对样本进行优化. 传统的CFSFDP聚类法往往通过人工在ρ-δ(局部密度ρ、距离δ)分布图中选择聚类中心,通过从簇中心权值变化趋势搜寻拐点的方式自动确定聚类中心,但采用不同的归一化函数计算后的簇中心权值γ所得到的聚类中心也不同[11]. 因此本文提出了分层CFSFDP聚类法,并以聚类中心作为最优样本. 分层原理如下.
① 对每个ROI中的样本进行粗过滤.
在计算ROI样本ρ和δ的均值和标准差的基础上,挑选满足莱茵达准则的样本点作为潜在聚类中心.
② 选择最优聚类中心.
对潜在聚类中心计算簇中心权值γ,择取最大γ值对应的点为第1个聚类中心y1,从潜在聚类中心点中提取距离第1个聚类中心点最近的点y2,计算距离D(y1,y2),如果D(y1,y2)>dc,那么点y2被确定为一个新的聚类中心点,否则提取次近点进行判断;再次提取距离点y1与点y2最近的点y3,若y3与y1、y2的距离满足
min[D(y1,y3),D(y2,y3)]>dc,
则y3为新的聚类中心,否则再次提取次近点进行判断;以此类推,直至遍布所有样本;所有满足要求的点作为最优聚类中心即最优样本.
3 隶属度均值聚类中心计算
通过分层峰值密度聚类方法,能够获取相同类别地物的不同样本集中心,但是由于同物异谱现象的存在,所形成的集合仍然会对后续分类算法产生一定的干扰. 为进一步抑制同物异谱现象的影响,本文采用了隶属度均值聚类法获取聚类中心点,实现对每类地物的均值向量集合优化. 考虑各个感兴趣样本向量属于每个类别的隶属度问题,通过计算各个样本向量属于每个类别的隶属概率或者隶属度,构建相应的隶属度矩阵,从而实现图像样本向量的聚类.
假设每类地物的均值向量集为MROIA={XA1,XA2,…,XAm}(m为A类的感兴趣区个数),隶属度函数是表示一个对象XAi隶属于A类的程度的函数,记做μA(xi),其自变量范围是所有可能属于A类的对象(即A类所在空间的所有点),取值范围是[0,1],μA(xi)≤1. 当μA(xi)=1时,表示XAi完全隶属于A类. 因此,算法的目标函数为
‖MROIj-xi‖2,
约束条件![]() 2)
2)
式中:隶属度矩阵μij为第i个样本向量数据第j类的隶属度;c为总类数;k为设置的参数,在本文中取2. 根据最优方法可以得出聚类中心的迭代公式为
MROIj=![]() .
.![]() 3)
3)
当满足条件max[J(n+1)-J(n)]<ε时,终止迭代运算,否则继续运行迭代计算. 最终输出聚类中心,完成聚类过程.
本文为了获取最优聚类中心向量,首先将MROIA中计算距离最远的c个向量作为初始类别中心,并计算隶属度函数,将m个向量分别归到c个类别中. 然后计算c个聚类中心均值,并将与均值距离最远的两类去除,以最大化消除干扰样本. 因此,最后余下c-2类样本就是最优代表向量样本.
4 实验及结果分析
本文选择美国EO-1卫星搭载的Hyperion高光谱传感器获取的青藏高原境内冰川的遥感图像为实验数据,对冰川、裸地和阴影等类别进行分类比较. 实验所用的遥感图像数据源共242个波段,光谱范围为0.4~2.5 μm,空间分辨率为30 m,光谱分辨率为10 nm,幅宽为7.7 km. 因为混淆矩阵可以表述出遥感影像中所有类别的错分与漏分精度,还可以计算出遥感影像的总体精度和Kappa系数. 因此,本文对分类结果进行了混淆矩阵精度分析.
以吉尔吉斯斯坦境内的阿赖山为研究区,地理位置为40°01'35.88″~40°07'39.38″N,73°49'29.12″~73°57'37.13″E,图1为研究区Hyperion高光谱影像校正后的(R(41)G(21)B(11))三波段合成图像. 最小距离分类、马氏距离分类与最优代表向量分类的分类结果如图2所示.
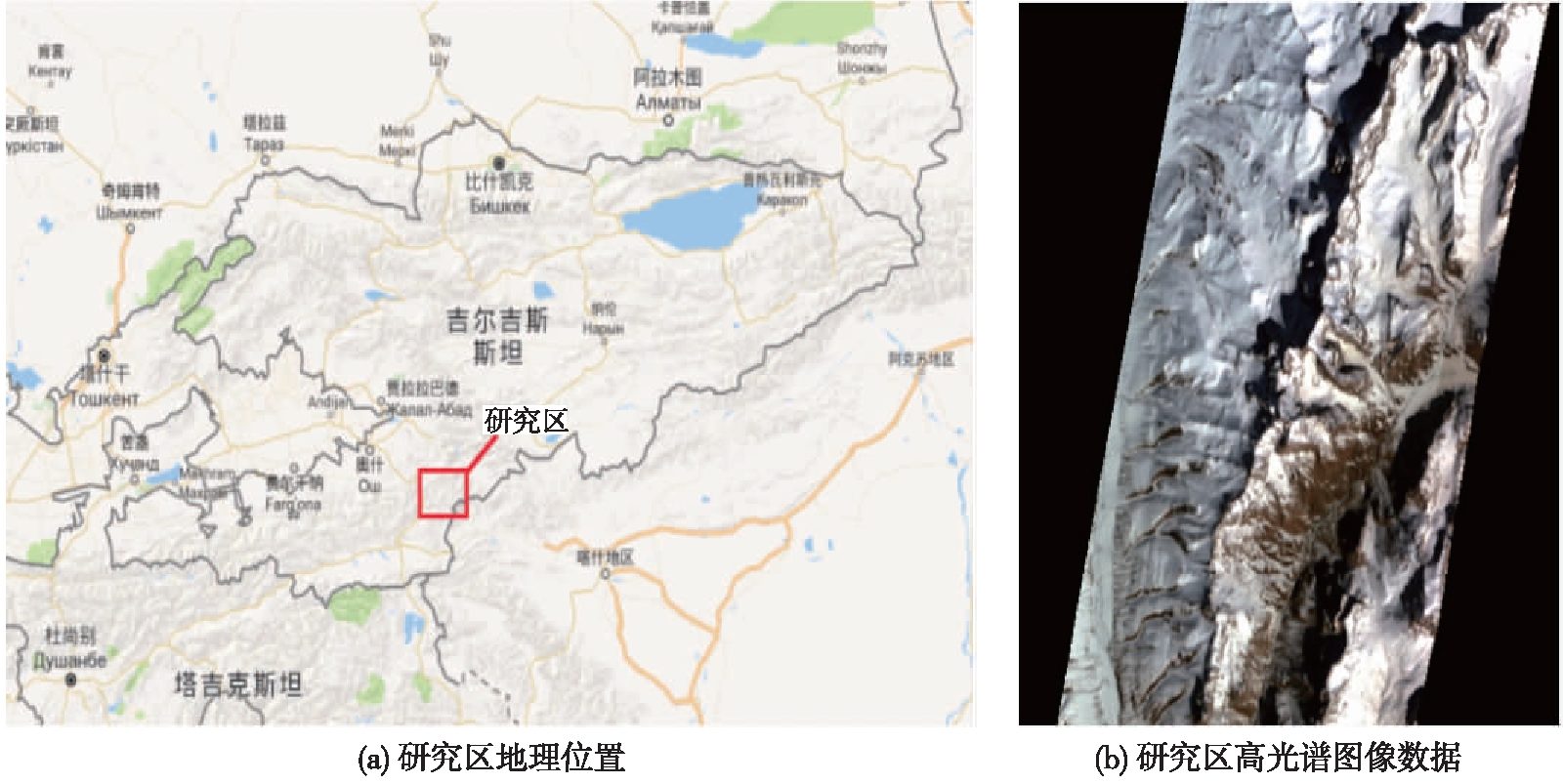
图1 阿赖山研究区高光谱图像数据
Fig.1 Hyperspectral image of study area of arlai
表1、表2和表3分别为最小距离分类法、马氏距离分类法和最优代表向量分类法的混淆矩阵.
表1 最小距离分类混淆矩阵
Tab.1 Confusion matrix of minimum distance classification
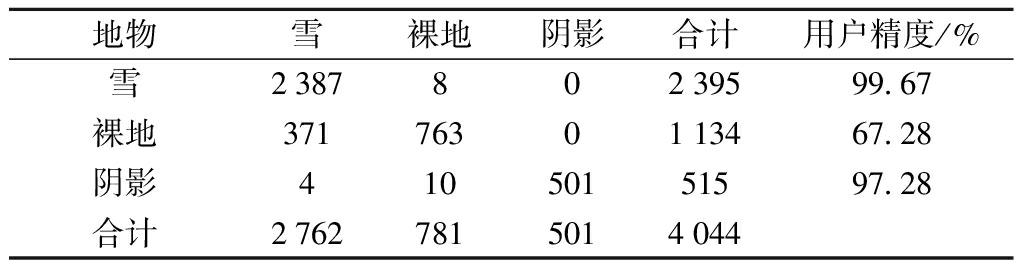
地物雪裸地阴影合计用户精度/%雪238780239599 67裸地3717630113467 28阴影41050151597 28合计27627815014044
注:雪,裸地,阴影的生产精度分别为86.42%,97.70%,100.00%.

图2 阿赖山分类结果图像
Fig.2 Classification result image of arlai
表2 马氏距离分类混淆矩阵
Tab.2 Confusion matrix of mahalanobis distance classification
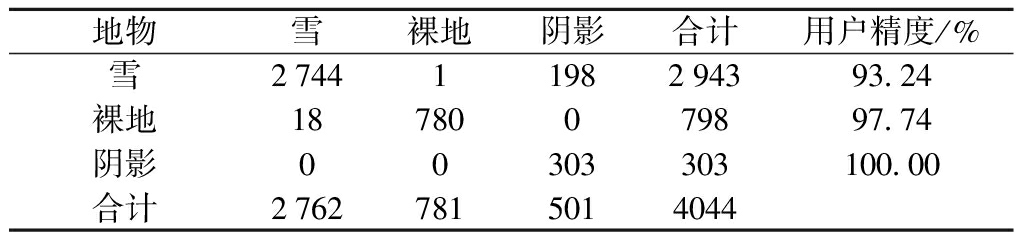
地物雪裸地阴影合计用户精度/%雪27441198294393 24裸地18780079897 74阴影00303303100 00合计27627815014044
注:雪,裸地,阴影的生产精度分别为99.35%,99.87%,60.47%.
表3 最优代表向量分类混淆矩阵
Tab.3 Confusion matrix of optimal representative vector classification
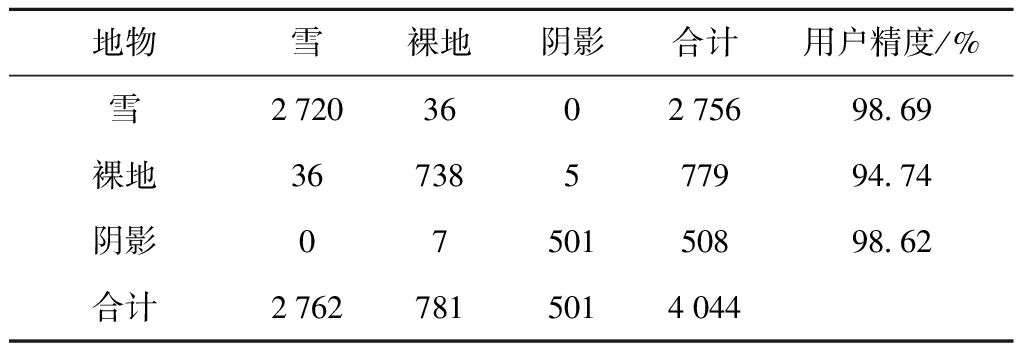
地物雪裸地阴影合计用户精度/%雪2720360275698 69裸地36738577994 74阴影0750150898 62合计27627815014044
注:雪,裸地,阴影的生产精度分别为98.48%,94.49%,100.00%.
本文还选择了西藏自治区普兰县和吉尔吉斯斯坦费尔干纳山作为研究区,分别获得各个研究区的分类混淆矩阵,并可以分别计算得出最小距离、马氏距离、最优代表向量等分类方法的总分类精度(overall accuracy)与Kappa系数. 对以上3组实验进行总体评价,得到结果如图3所示.
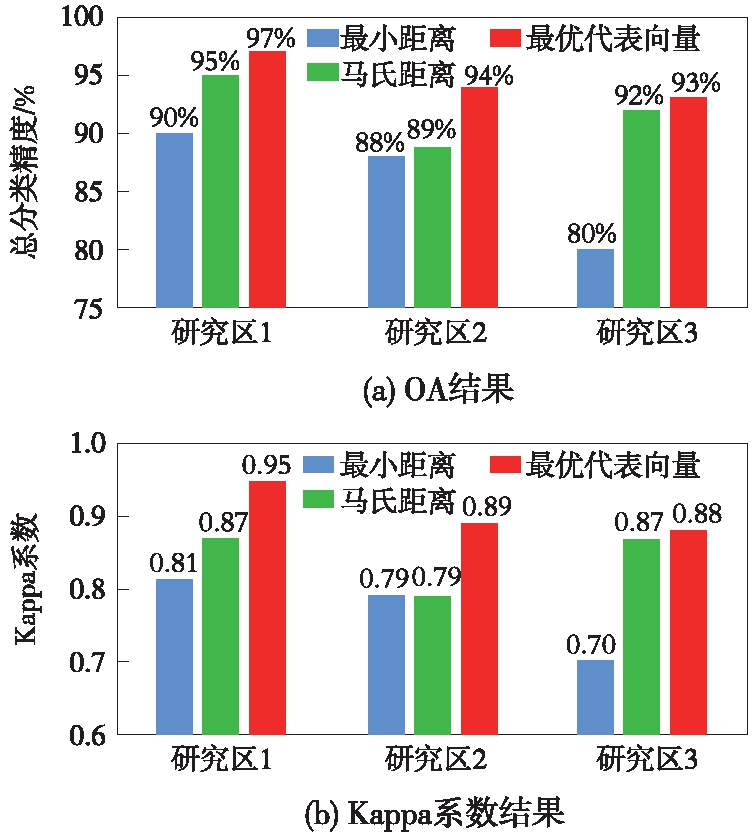
图3 实验数据分类评价
Fig.3 Classification evaluation of experimental datas
从实验数据总体分类评价图中能够看出,最小距离分类法的总体精度为86%,Kappa系数为0.77;马氏距离分类法的总体精度为92%,Kappa系数为0.84;最优代表向量分类法的总体分类精度为94%,Kappa系数为0.91. 同时,分类结果表明马氏距离分类法不仅考虑了类别的均值向量,而且考虑了各特征点在类别中心周围分布的情况,分类精度相比于最小距离分类法有了很大提高,但对于阴影区域比较敏感,识别精度不高;最优代表向量分类法可以准确识别阴影区域,总体分类精度明显高于最小距离分类法和马氏距离分类法,有效地提高了高光谱遥感影像的冰川分类精度.
5 结 论
本文针对高光谱遥感图像在冰川分类中样本代表性差、识别范围相交的问题,提出了基于最优代表向量的冰川分类算法,重点对训练样本进行最大程度优化,利用密度峰值聚类进行感兴趣样本选择,并对样本均值向量进行隶属度均值聚类择优,有效消除了同物异谱的干扰,并解决样本选取差异对分类结果影响大的问题. 通过对青藏高原吉尔吉斯斯坦与西藏自治区境内的冰川数据进行实验验证,可以看最优代表向量方法有效提高了高光谱遥感图像冰川分类精度. 在下一步的工作中,将继续开展高光谱遥感图像分类实验验证,希望最优代表向量法能够在农业、林业、军事等不同领域得到应用.
参考文献:
[1] 吴珊珊,姚治君,姜丽光,等.现代冰川体积变化研究方法综述[J].地球科学进展,2015,30(2):237-246.
Wu Shanshan, Yao Zhijun, Jiang Liguang, et al. Method review of modern glacier volume change[J]. Advances in Earth Science, 2015,30(2):237-246. (in Chinese)
[2] Goetz A F H. Three decades of hyperspectral remote sensing of the earth: a personal view[J]. Remote Sensing of Environment, 2009,113(S1):5-16.
[3] Chang C I. Hyperspectral imaging: techniques for spectral detection and classification[M]. New York: Plenum Publishing Co, 2003.
[4] 胥海威,杨敏华,韩瑞梅,等.用随机决策树群算法进行高光谱遥感影像分类[J].应用科学学报,2011,29(6):598-604.
Xu Haiwei, Yang Minhua, Han Ruimei, et al. Hyperspectral remote sensing image classification with extremely randomized clustering forests[J]. Journal of Applied Sciences, 2011,29(6):598-604. (in Chinese)
[5] 李光辉,王成,郑照军,等.机载高光谱数据冰川分类方法研究——以“中习一号”冰川为例[J].遥感技术与应用,2013,28(5):766-772.
Li Guanghui, Wang Cheng, Zheng Zhaojun, et al. Study on glacier classification methods of airborne hyperspectral data——a case study of the zhongxi-1 glacier[J]. Remote Sensing Technology and Application, 2013,28(5):766-772. (in Chinese)
[6] 赵健赟,彭军还. 于Landsat TM影像的山地冰川信息提取技术研究[J].华中师范大学学报:自科版,2016,50(2):309-313.
Zhao Jianyun, Peng Junhuan. Information extraction technologies of mountainous glacier based on Landsat TM image[J]. Journal of HuaZhong Normal University: Natural Sciences ed, 2016,50(2):309-313. (in Chinese)
[7] Narama C, Shimamura Y, Nakayama D, et al. Recent changes of glacier coverage in the western Terskey-Alatoo range, Kyrgyz Republic, using Corona and Landsat[J]. Annals of Glaciology, 2006,43(1):223-229.
[8] Gjermundsen E F, Mathieu R, Kääb A, et al. Assessment of multispectral glacier mapping methods and derivation of glacier area changes, 1978-2002, in the central Southern Alps, New Zealand, from ASTER satellite data, field survey and existing inventory data[J]. Journal of Glaciology, 2011,57(204):667-683.
[9] Raza I U R, Kazmi S S A, Ali S S, et al. Comparison of pixel-based and object-based classification for glacier change detection[J]. Earth Observation and Remote Sensing Applications, 2012:259-262.
[10] Rodriguez A ,Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014,344(6191):1492-1496.
[11] 马春来,单洪,马涛.一种基于簇中心点自动选择策略的密度峰值聚类算法[J].计算机科学, 2016, 43(7): 255-258.
Ma Chunlai, Shan Hong, Ma Tao. Improved density peaks based clustering algorithm with strategy choosing cluster center automatically[J]. Computer Science, 2016,43(7):255-258. (in Chinese)
Optimal Representative Vector Method and Its Application for Glacier Classification
Abstract: The existence of synonyms spectrum phenomenon and the poor sample representativeness and parameter setting in the classification process result in the unstable classification result and poor classification accuracy of hyperspectral images. In order to solve this problem, a novel optimal representative vectors classification algorithm based on sample set optimization was proposed for glacier classification. This algorithm purified original samples in the ROI through an improved density peak clustering method, and selected the optimal representative vectors by clustering the mean vector set of optimized samples as the central vector of each object. Through experimental verification, this algorithm can effectively improve the classification accuracy of the glacier to 90%; it shows that the optimal representative vectors classification method can eliminate the impact of sample differences and improve glacier classification accuracy.
Key words: hyperspectral remote sensing; image classification; optimal representative vector; density peak clustering; glacier classification
收稿日期: 2017-06-21
基金项目: 高分辨率对地观测系统重大专项基金资助项目;“十三五”武器装备预研领域基金资助项目;中央高校基本科研业务费专项资金资助项目(FRF-TP-15-117A1);中国博士后科学基金资助项目(2016M600922)
中图分类号: TP 751.1
文献标志码: A
文章编号:1001-0645(2017)10-1067-05
DOI:10.15918/j.tbit1001-0645.2017.10.014
(责任编辑:刘雨)
