基于多源遥感影像的南极Lambert流域冰川运动速度提取与精度验证
【类型】期刊
【作者】刘爽,童小华(同济大学测绘与地理信息学院;同济大学空间信息科学与可持续发展应用中心)
【作者单位】同济大学测绘与地理信息学院;同济大学空间信息科学与可持续发展应用中心
【刊名】同济大学学报(自然科学版)
【关键词】 冰川运动速度;差分干涉技术;多孔径干涉技术;Lambert冰川;精度验证
【资助项】国家“九七三”重点基础研究发展计划(2012CB957701);国家杰出青年科学基金(41325005)
【ISSN号】0253-374X
【页码】P394-400
【年份】2019
【期号】第3期
【期刊卷】1;|6;|7;|8;|4;|5;|2
【摘要】冰川运动速度是计算极地物质平衡和对冰盖和冰架数值模拟的重要参数.针对传统冰川运动速度提取算法的不足和局限,基于差分干涉技术(DInSAR)和多孔径干涉技术(MAI)开展二维冰川运动速度的提取研究.将该算法应用于南极Lambert流域冰川运动速度的提取,得到了研究区域高精度的二维冰川运动速度场,将采用偏移量跟踪算法提取的冰川运动速度和本文提取的冰川运动速度进行了对比分析和精度评价;结合研究区域已有历史观测数据,分析全球气候变化背景下Lambert流域冰川的动态变化.研究结果表明,基于DInSAR和MAI的冰川运动速度提取算法优于偏移量跟踪算法;近20年的冰川运动速度时间序列数据显示Lambert流域的冰川运动速度基本处于稳定状态.
【全文】 文献传递
基于多源遥感影像的南极Lambert流域冰川运动速度提取与精度验证
摘要: 冰川运动速度是计算极地物质平衡和对冰盖和冰架数值模拟的重要参数.针对传统冰川运动速度提取算法的不足和局限,基于差分干涉技术(DInSAR)和多孔径干涉技术(MAI)开展二维冰川运动速度的提取研究.将该算法应用于南极Lambert流域冰川运动速度的提取,得到了研究区域高精度的二维冰川运动速度场,将采用偏移量跟踪算法提取的冰川运动速度和本文提取的冰川运动速度进行了对比分析和精度评价;结合研究区域已有历史观测数据,分析全球气候变化背景下Lambert流域冰川的动态变化.研究结果表明,基于DInSAR和MAI的冰川运动速度提取算法优于偏移量跟踪算法;近20年的冰川运动速度时间序列数据显示Lambert流域的冰川运动速度基本处于稳定状态.
关键词: 冰川运动速度; 差分干涉技术; 多孔径干涉技术; Lambert冰川; 精度验证
冰川运动速度是冰川运动的重要指标,是计算极地物质平衡[1-5]、冰盖与冰架数值模拟的重要参数.传统的冰川运动速度提取技术如花杆测量、GPS等[6-11]仅能获取局部区域的离散观测数据.光学遥感易受极地极夜、太阳辐射、云雾及影像过饱和等约束.合成孔径雷达(SAR)采用主动式的微波成像模式,可以实现全天时、全天候的对地观测[4, 12-13],在冰川运动速度提取中占据着重要的地位[14-15],是目前冰川运动速度提取的主要手段.
传统的差分干涉技术能够获取雷达视线向的高精度地表形变,但是对影像方位向的地表运动不敏感.为了弥补传统差分干涉雷达(DInSAR)技术在方位向地表形变提取中的不足和局限,2006年Bechor 等[16]提出了多孔径干涉测量技术(MAI),用于方位向地表形变位移的提取.由于其能够获取高精度的方位向地表位移,因此广泛应用于地震、滑坡等灾害的变形监测[17-18].已有的研究结果表明,MAI提取的方位向的地表位移优于偏移量跟踪算法获取的方位向地表形变,但是MAI算法无法获取影像距离向的地表位移.因此,本文采用DInSAR和MAI算法开展高精度冰川运动速度的提取及精度验证研究,并结合多源遥感影像数据获取的冰川运动速度分析全球气候变化背景下Lambert流域冰川运动速度的动态变化.
1 DInSAR和MAI冰川运动速度提取
综合考虑DInSAR和MAI在地表形变提取中的优越性及存在的不足,采用DInSAR技术提取距离向的冰川运动速度,利用MAI获取方位向的冰川运动速度,然后构建冰川运动速度的偏差改正模型,并利用研究区域的岩石点对DInSAR和MAI提取的冰川运动速度进行偏差改正和精度评估研究,最后结合研究区域已有的研究成果,开展Lambert流域冰川运动速度的动态分析.
1.1 数据预处理
为了提高数据处理的效率和减小数据后处理带来的拼接和镶嵌误差,首先对同一轨道相邻的多景欧洲遥感卫星(ERS-1/2)数据进行拼接和镶嵌,然后对拼接之后的原始数据进行成像处理,获取拼接之后的单视复数(SLC)影像数据.
1.2 距离向冰川运动速度提取
基于DInSAR的基本原理,干涉相位Δφint由地表地形相位Δφtopo、形变信息Δφdisp、平地相位Δφflat、大气延迟相位Δφatom以及系统热噪声产生的随机相位Δφnoise等组成,如下所示:
Δφint=Δφtopo+Δφflat+Δφdisp+Δφatom+Δφnoise
(1)
为了获取仅含地表形变信息的差分干涉相位,必须对干涉相位进行差分干涉处理,消除干涉相位中的地形相位,获取雷达视线向的地表形变.同时,考虑卫星的入射角,获取距离向的地表形变位移场.本文选取卫星精密星历轨道数据(PRC)及数字高程模型(DEM),采用“二轨法”对干涉像对进行差分干涉处理,消除干涉相位中的地形相位,开展距离向冰川运动速度提取.
1.3 方位向冰川运动速度提取
为获取方位向高精度的地表形变位移场,2006年Bechor等[16]提出了多孔径干涉技术,其基本原理如下.
假设地面物体沿着卫星的方位向具有位移x,则其在前视向和后视向干涉图中的干涉相位(如图1所示)分别为
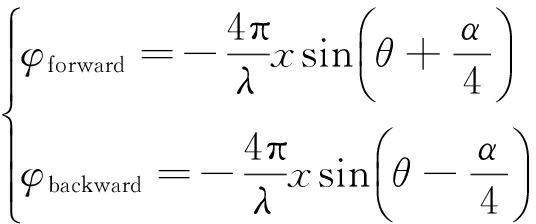
(2)
式中:φforward 、φbackward 分别为前视向和后视向的干涉相位;θ为雷达视线方向与飞行方向的夹角;α为雷达视线方向的偏角.
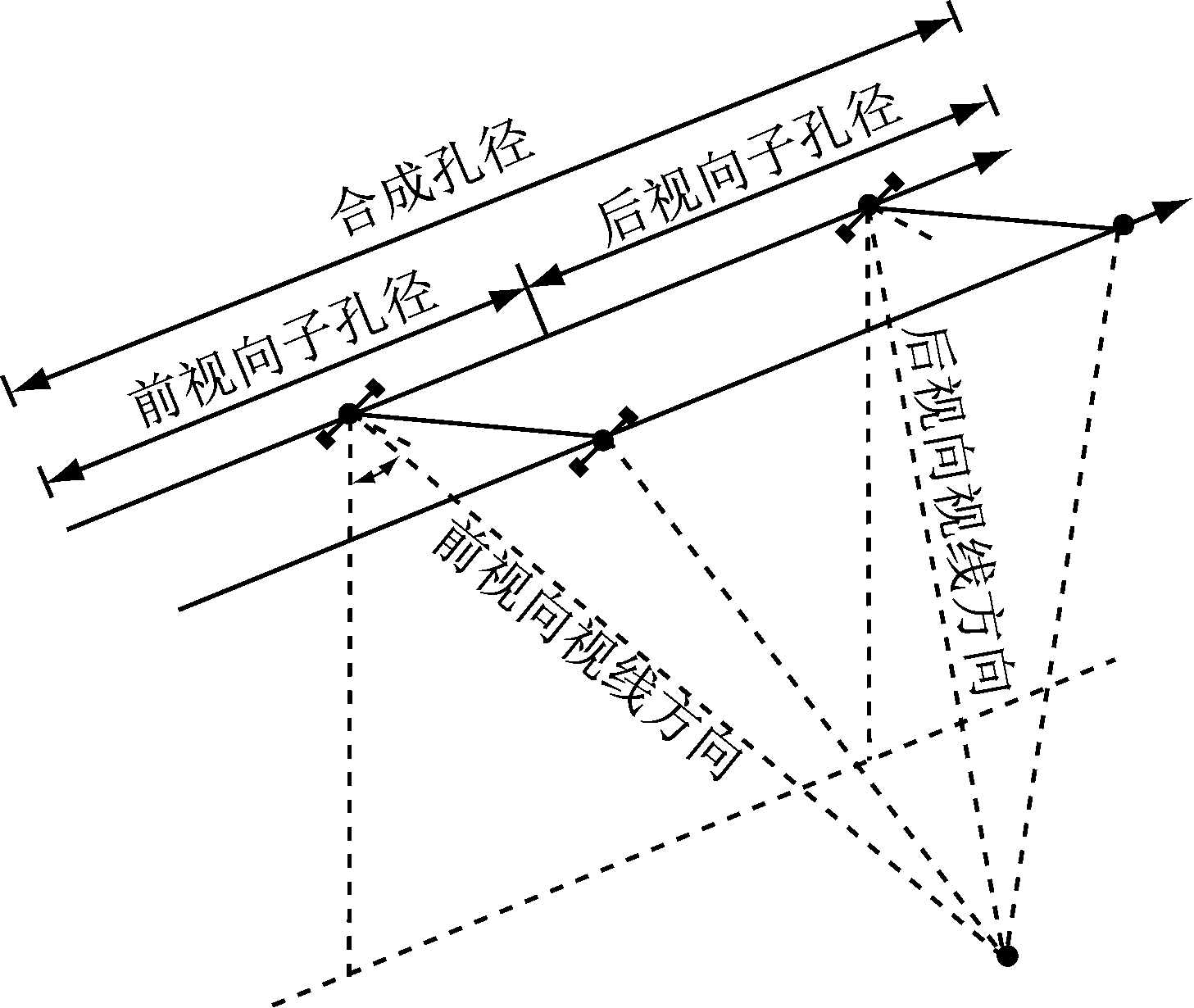
图1 MAI基本原理示意图
Fig.1 Principle of multiple aperture interferometry
对前视向和后视向干涉相位进行差分处理,则可以消除两者中共同的地形相位、平地相位的影响,获取仅反映方位向地表位移的MAI干涉相位φMAI.
(3)
由于α和θ均非常小,同时α≈λ/l(l为SAR天线的长度),则方位向地表位移所引起的MAI干涉相位可以表达为
(4)
1.4 冰川运动速度偏差建模与补偿
受大气延迟误差、外部DEM误差及基线误差的影响,方位向和距离向的冰川运动速度不可避免含有残余地形相位和线性相位趋势项,为了提高方位向和距离向的冰川运动速度的估算精度,提出基于二次多项式的偏差补偿模型:
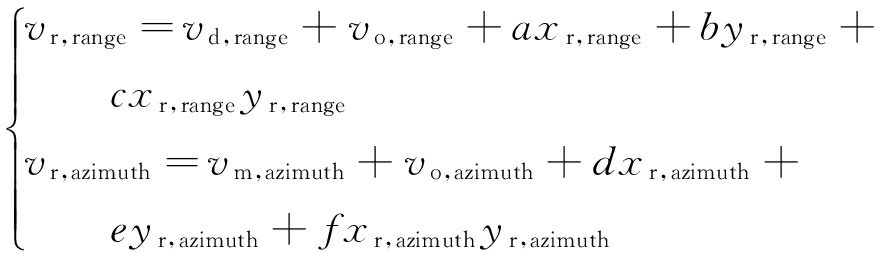
(5)
式中:vr,range、vr,azimuth分别为基准点在距离向和方位向的冰川运动速度;vd,range、vm,azimuth分别为DInSAR和MAI估计的距离向和方位向的冰川运动速度;vo,range、vo,azimuth分别为距离向和方位向的冰川运动速度的系统偏差;(xr,range,yr,range)与(xm,azimuth,ym,azimuth)分别为基准点在SAR影像的距离-多普勒坐标系下的坐标;a,b,c,d,e,f为多项式偏差补偿模型的系数.受极端环境条件的约束,本文选取岩石点作为基准点进行偏差补偿模型系数的求解.
2 研究区域及实验数据
Lambert流域位于Amery冰架的上游区域(图2),主要由Lambert冰川、Mellor冰川及Fisher冰川组成,其中Lambert冰川被认为是世界上最大的冰川,有100 km宽,400 km长,冰厚度约2 500 m,是南极内陆物质注入海洋的主要通道.
考虑由于冰川运动导致的SAR影像间的影像失相关,采用ERS-1/2卫星串行模式的SAR影像数据开展冰川运动速度的提取研究,本文的实验数据如表1所示.此外,为了对Lambert流域的冰川运动状态进行动态分析,本文对2013—2014年的Landsat 8 陆地成像仪(OLI)获取的遥感影像数据采用偏移量跟踪算法进行处理,提取二维冰川运动速度场,数据的基本信息如表1所示.
表1 研究区域的遥感影像数据
Tab.1 Datasets of the area studied
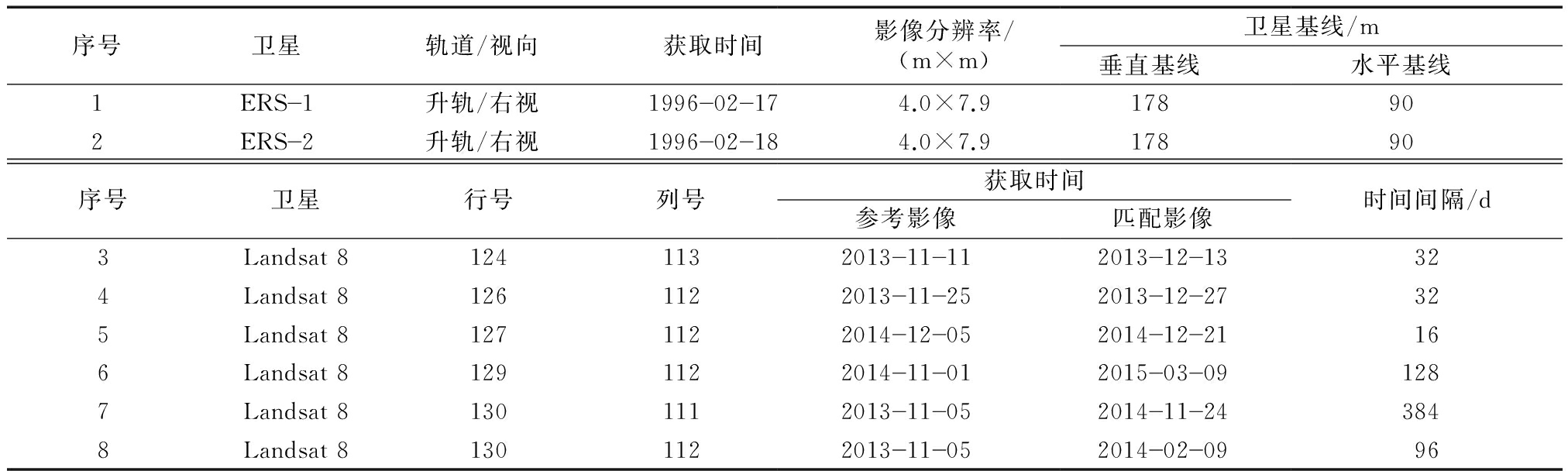
序号卫星轨道/视向获取时间影像分辨率/(m×m)卫星基线/m垂直基线水平基线1ERS1升轨/右视199602174.0×7.9178902ERS2升轨/右视199602184.0×7.917890序号卫星行号列号获取时间参考影像匹配影像时间间隔/d3Landsat81241132013111120131213324Landsat81261122013112520131227325Landsat81271122014120520141221166Landsat812911220141101201503091287Landsat813011120131105201411243848Landsat8130112201311052014020996
从表1可以看出,ERS-1/2的影像的方位向分辨率为4.0 m,距离向分辨率为7.9 m.其中干涉像对分别于1996年2月17日和1996年2月18日获取,垂直基线为178 m.研究区域共有12景Landsat 8遥感影像,其获取日期为2013年11月到2015年3月,共6个像对,平均时间间隔为115 d,最短时间间隔为16 d,最长时间间隔为384 d.
此外,为了消除干涉相位中的地形相位,获取仅含地表冰川运动所引起的差分干涉相位,选取基于南极ERS-1雷达测高和美国冰、云和陆地高程卫星激光测高数据获取的南极DEM数据[19]进行地形相位的模拟和差分干涉数据处理,该DEM数据的空间分辨率为1 km,在接地线处的垂直精度为5 m.
3 实验结果分析与精度验证
3.1 Lambert流域冰川运动速度
为了提取Lambert流域的冰川运动速度,首先采用基于DEM数据的SAR影像配准算法,实现SAR影像的配准精度优于0.02个像素.然后对配准之后的影像进行差分干涉处理,获取由于冰川运动所产生的差分干涉相位,如图2a所示,并采用最小网络费用流(MCF)相位解缠算法[20]对差分干涉相位进行相位解缠,采用岩石点利用本文提出的偏差改正模型进行补偿,最后考虑卫星的入射角及时间间隔将获取的解缠相位转换为距离向的地表冰川运动速度场(如图2b所示).
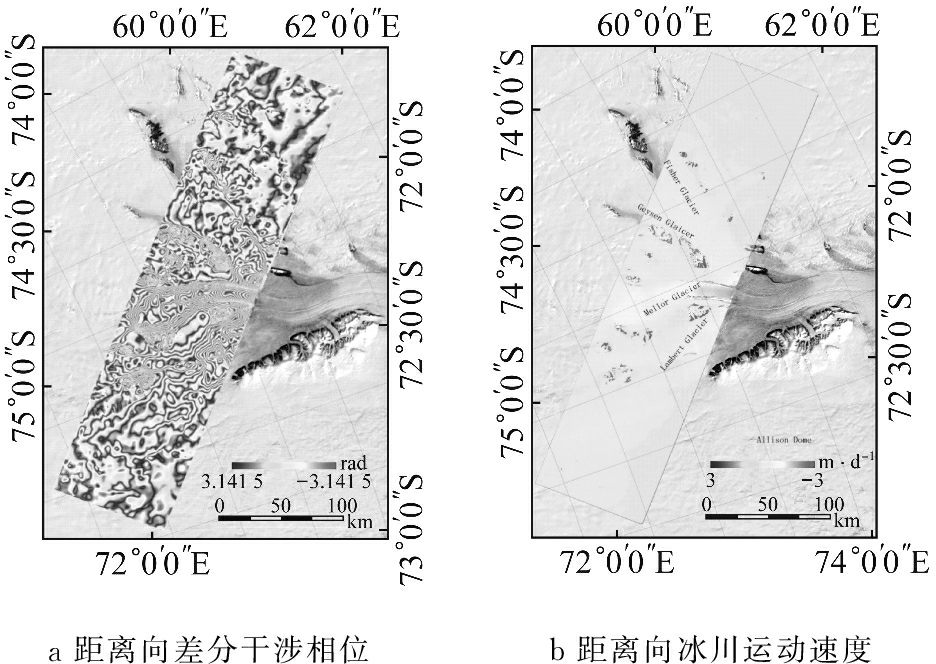
a距离向差分干涉相位b距离向冰川运动速度
图2 距离向差分干涉相位及冰川运动速度
Fig.2 Differential interferogram and ice flow velocity in the range direction estimated by using the DInSAR method
为了获取方位向的冰川运动速度,首先采用分频算法对SAR干涉像对进行分频处理,获取前视向和后视向SLC影像数据.然后对配准后的影像进行干涉处理,获取前视向和后视向的干涉相位,对前视向和后视向的干涉相位进行方位向的差分处理可以获取仅含有方位向地表位移的MAI干涉相位,如图3a所示,采用MCF算法对MAI干涉相位进行相位解缠处理,并对方位向的解缠相位采用岩石点进行偏差改正和补偿,获取方位向的冰川运动速度场,如图3b所示.
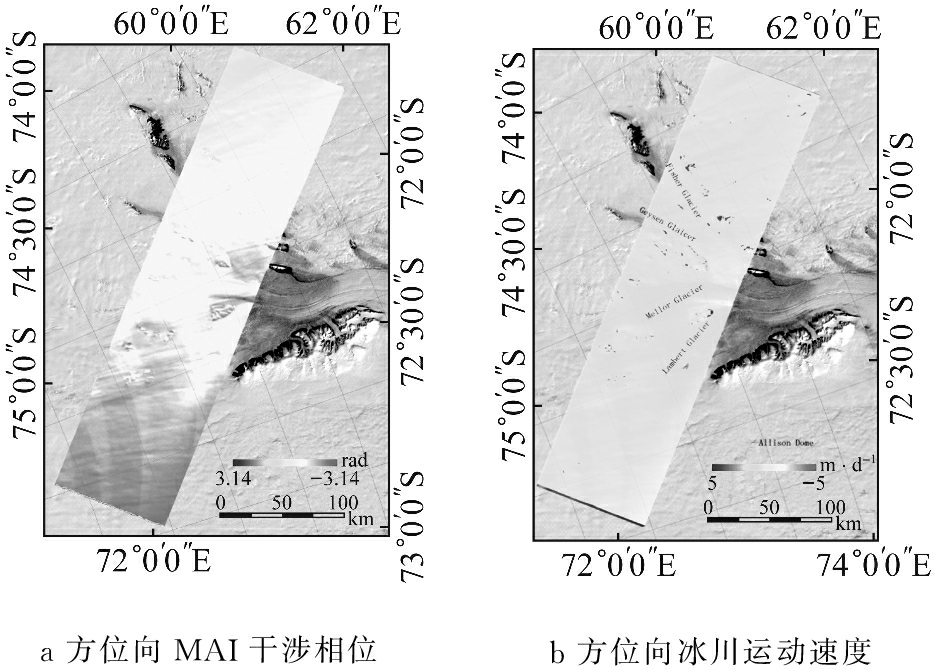
a方位向MAI干涉相位b方位向冰川运动速度
图3 方位向MAI干涉相位及冰川运动速度
Fig.3 MAI interferogram and the estimated ice flow velocity in the azimuth direction by using the MAI method
为了对DInSAR和MAI算法提取的冰川运动速度进行验证,对研究区域2013—2014年间的Landsat 8 的15 m分辨率的全色波段影像采用偏移量跟踪算法进行处理和分析,获取研究区域的二维冰川运动速度.其中匹配窗口的大小为32像素×32像素,行方向和列方向的采样间隔为10像素,并采用信噪比为0.95剔除误匹配点.考虑影像之间的时间间隔,同时对多景影像的处理结果进行拼接镶嵌,获取研究区域偏移量跟踪算法提取的二维冰川运动速度,如图4所示.
从图4可以看出,偏移量跟踪算法可以有效地提取研究区域的二维冰川运动速度,其提取的冰川运动速度的空间分辨率为150 m.对比DInSAR与MAI提取的距离向和方位向的冰川运动速度(图2b和图3b),可以发现,两者之间基本一致,只是由于影像数据获取的季节不同,仅在局部区域存在细微的差异.同时,假设岩石点处的冰川运动速度为0 m·d-1,并采用岩石点为基准,分别从偏移量跟踪算法和本文算法获取的冰川运动速度场中提取研究区域的岩石基准点处的冰川运动速度,计算其标准差.研究结果表明,采用DInSAR和MAI算法提取的冰川运动速度距离向精度为0.01 m·d-1, 方位向精度为0.07 m·d-1,而偏移量跟踪算法获取的冰川运动速度在距离向和方位向的精度分别为0.16 m·d-1 和0.13 m·d-1,因此本文采用DInSAR与MAI算法的冰川运动速度提取算法的精度优于传统的偏移量跟踪算法.
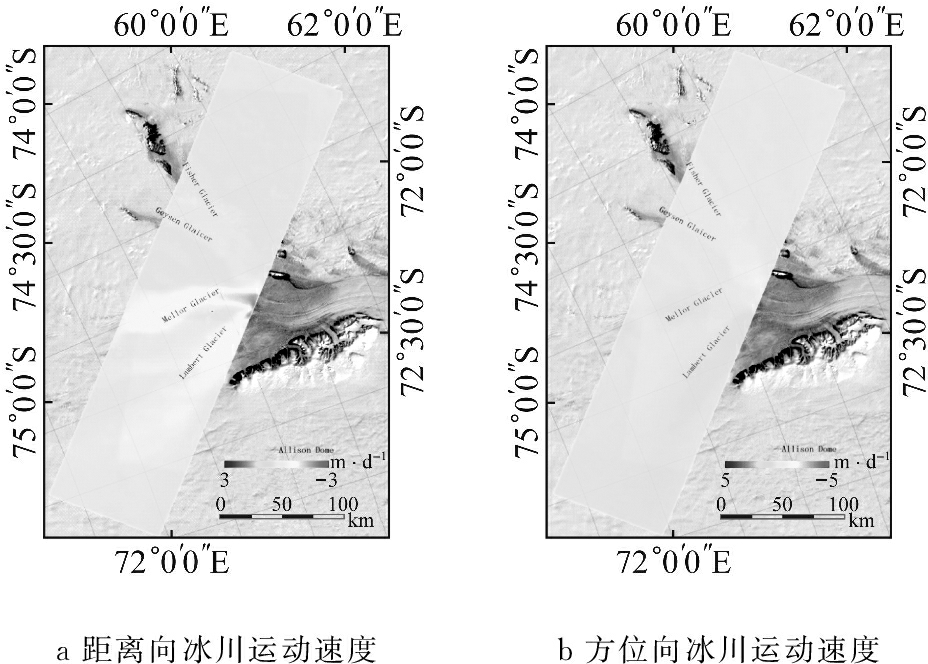
a距离向冰川运动速度b方位向冰川运动速度
图4 偏移量跟踪算法的距离向和方位向冰川运动速度
Fig.4 Two dimensional ice flow velocity obtained from Landsat 8 images using the offset tracking method
3.2 冰川运动速度精度评价与动态分析
由于研究区域缺少必要的同步地面观测数据,此外,研究区域的已有成果与本文的结果之间存在数据源及时间的差异,因此本文假设岩石点处的冰川运动速度为0 m·d-1,并作为基准数据开展冰川运动速度的精度评价.
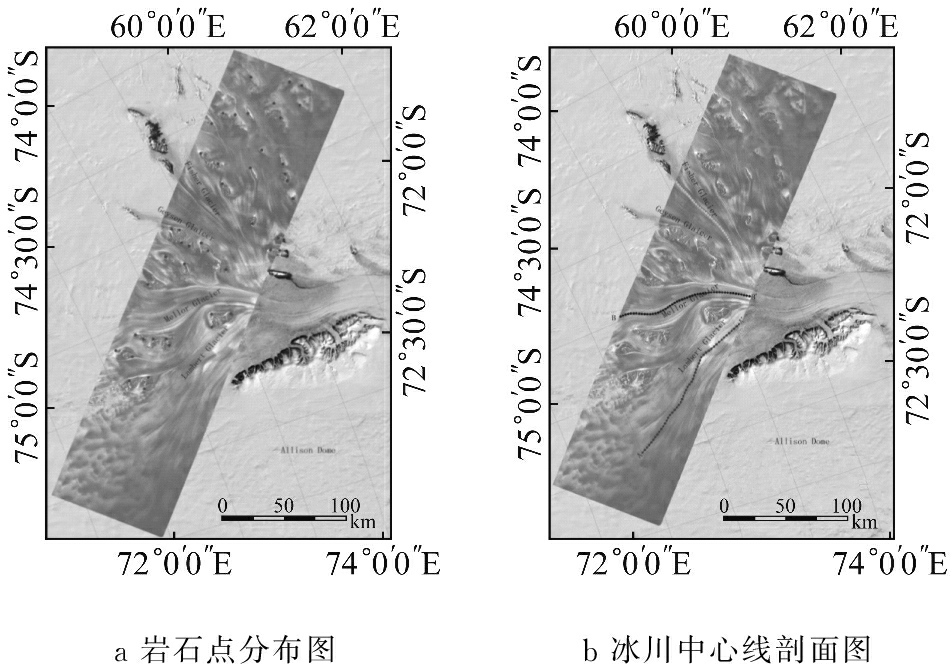
a岩石点分布图b冰川中心线剖面图
图5 研究区域岩石点的分布图及剖面位置示意图
Fig.5 Location and profiles of rock points
本文首先基于SAR强度影像进行岩石点的识别与选取,然后利用南极的中分辨率成像光谱仪(MODIS)数据的镶嵌影像对选取的岩石点进行进一步的检核,最后利用岩石点附近冰川运动速度接近于0 m·d-1的窗口区域计算均值和标准差,对残差大于3倍标准差的岩石点进行剔除.最后采用选取的30个岩石基准点(如图5a所示)对DInSAR和MAI的结果进行精度评估,其中距离向冰川运动速度的精度为0.10 m·d-1,方位向冰川运动速度的精度为0.07 m·d-1.
此外,为了分析全球气候变化背景下,Lambert流域的冰川运动速度的变化特征,将本文获取的Lambert冰川、Mellor冰川和Fisher冰川沿冰川运动中线处的距离向和方位向冰川运动速度(如图5b所示),与Jezek[21]利用偏移量跟踪算法对1997和2000年卫星南极制图项目(RAMP)期间获取的Radarsat-1数据进行处理而获取的冰川运动速度和Rignot等[22-23]利用Speckle跟踪算法对2007—2009年国际极地年(IPY)期间获取的多源SAR影像数据处理而获取的冰川运动速度进行对比分析,结果如图6、图7和图8所示.
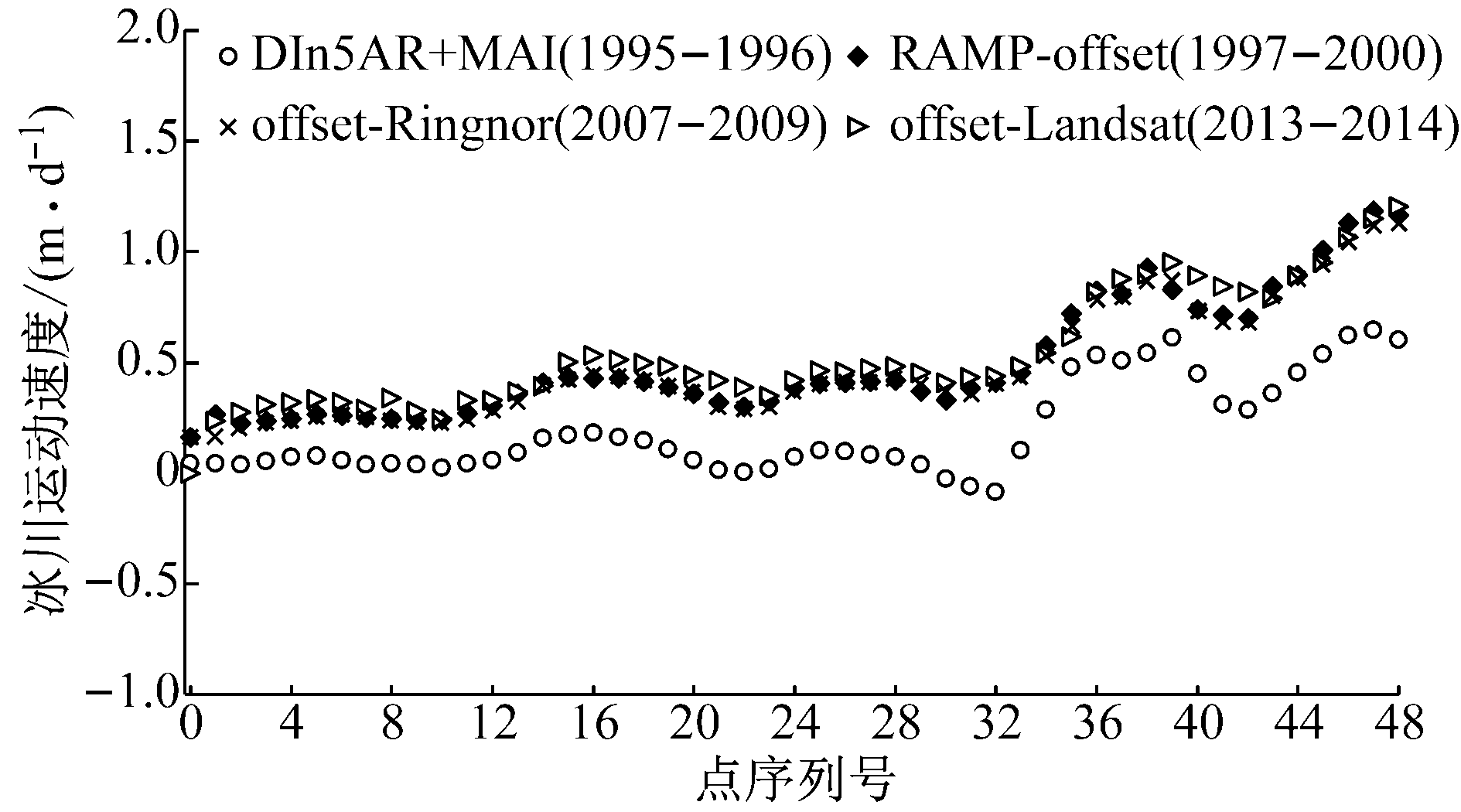
a Lambert冰川距离向冰川运动速度
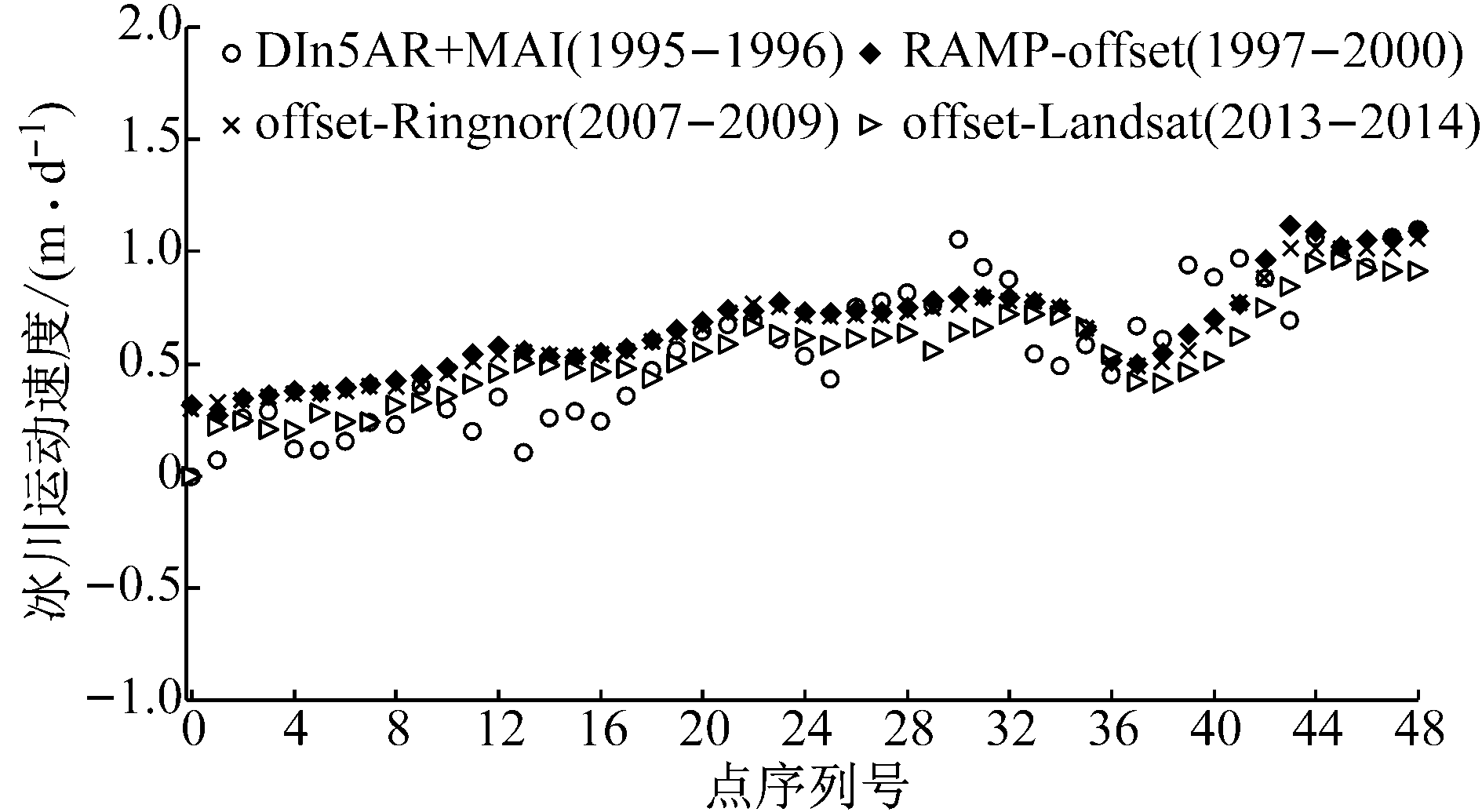
b Lambert冰川方位向冰川运动速度
图6 Lambert冰川运动速度对比分析
Fig.6 Ice flow velocity along the profile ofLambert Glaciers
从图6可以看出,沿着冰川运动方向,Lambert冰川的冰川运动速度逐渐增加.在距离向,前端冰川的运动速度为0.1 m·d-1,而末梢冰川运动速度的最大值为1.5 m·d-1; 而在方位向,冰川运动速度从0.3 m·d-1逐渐增加到1.2 m·d-1. 从长时间序列的数据看,在过去的20年间,Lambert冰川在距离向的冰川运动速度呈现缓慢的加速趋势,相对于1995—1996年度而言,Lambert冰川运动速度平均增加了0.5 m·d-1.而方位向的冰川运动速度基本保持一致.
从图7可以看出,在距离向,Mellor冰川沿着冰川运动方向运动速度由0.5 m·d-1逐渐增加到2 m·d-1;而在方位向,冰川的运动速度先减速,然后逐渐加速到0.5 m·d-1, 再减速一直到冰川的末梢.从时间序列上看,在过去的20年间,Mellor冰川的运动速度基本保持不变,但是在方位向,冰川的运动速度则有轻微的减速.
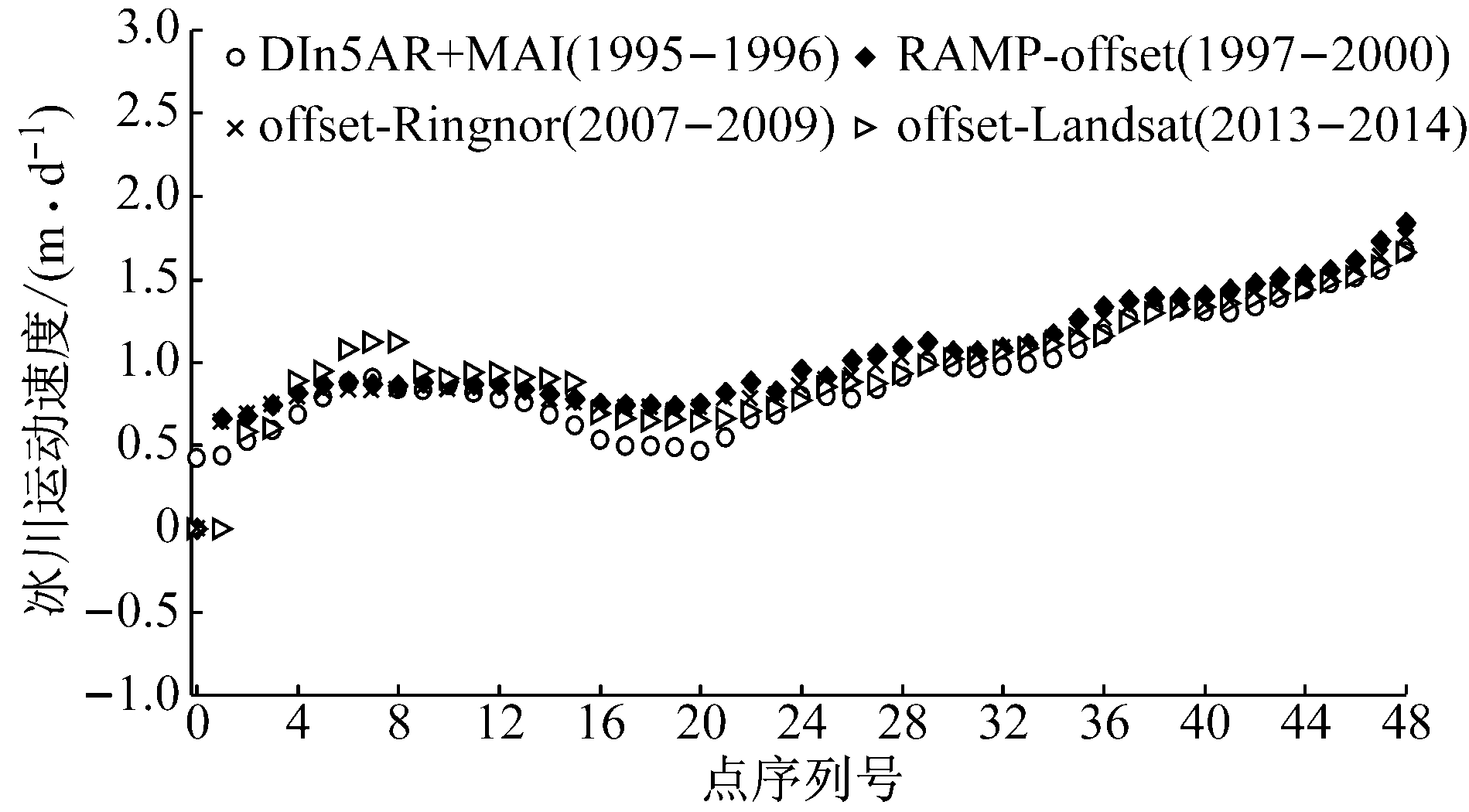
a Mellor冰川距离向冰川运动速度
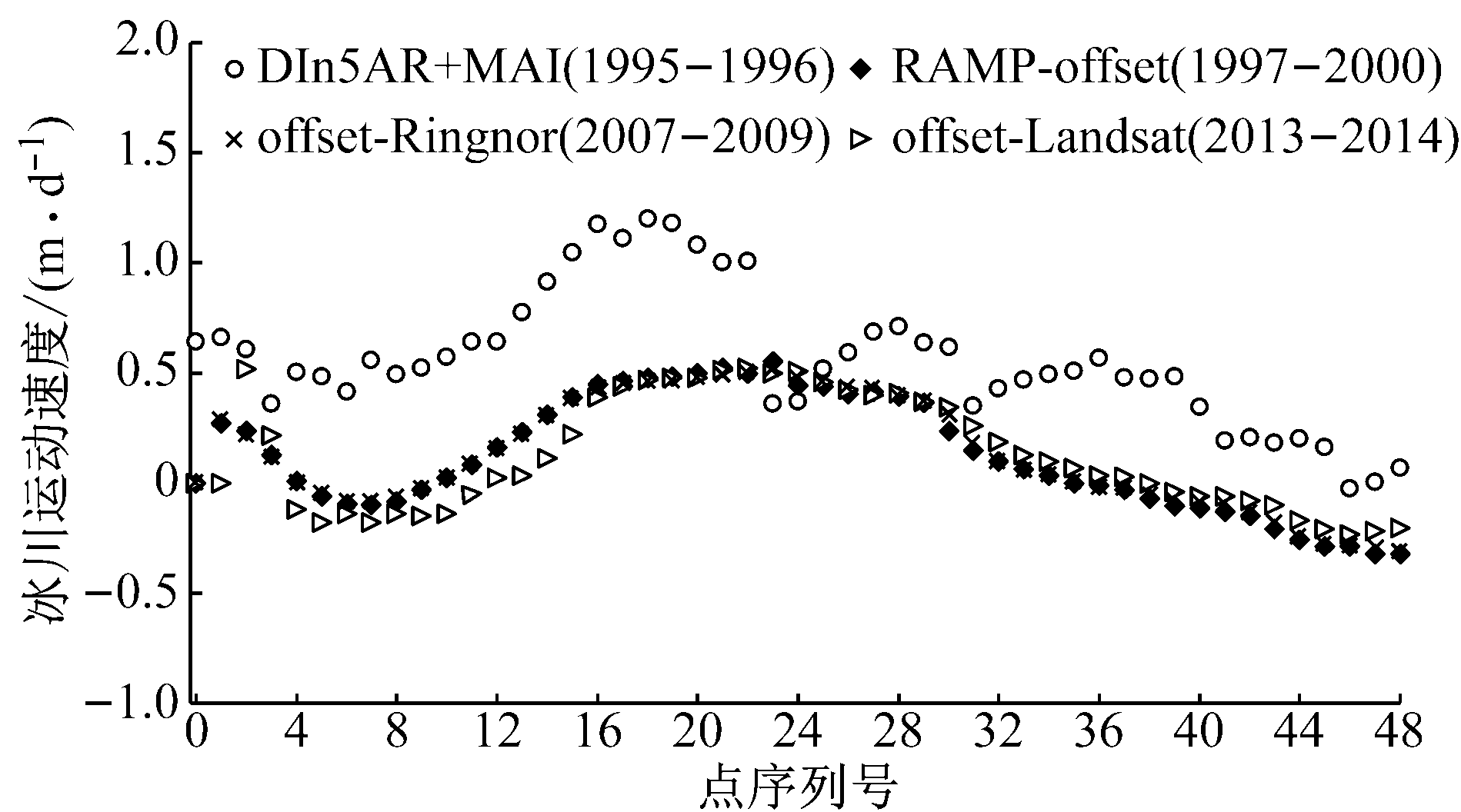
b Mellor冰川方位向冰川运动速度
图7 Mellor冰川运动速度对比分析
Fig.7 Ice flow velocity along the profile ofMellor Glaciers
从图8可以看出,Fisher冰川的冰川运动速度基本稳定,沿着冰川运动方向,距离向和方位向的冰川运动速度均呈现轻微的加速,距离向冰川运动速度的最大值为1.0 m·d-1,而方位向冰川运动速度的最大值为0.8 m·d-1.从时间序列上分析,可以发现在过去的20年间,Fisher冰川的运动速度整体上保持稳定,但是有轻微的减速的趋势.

a Fisher冰川距离向冰川运动速度
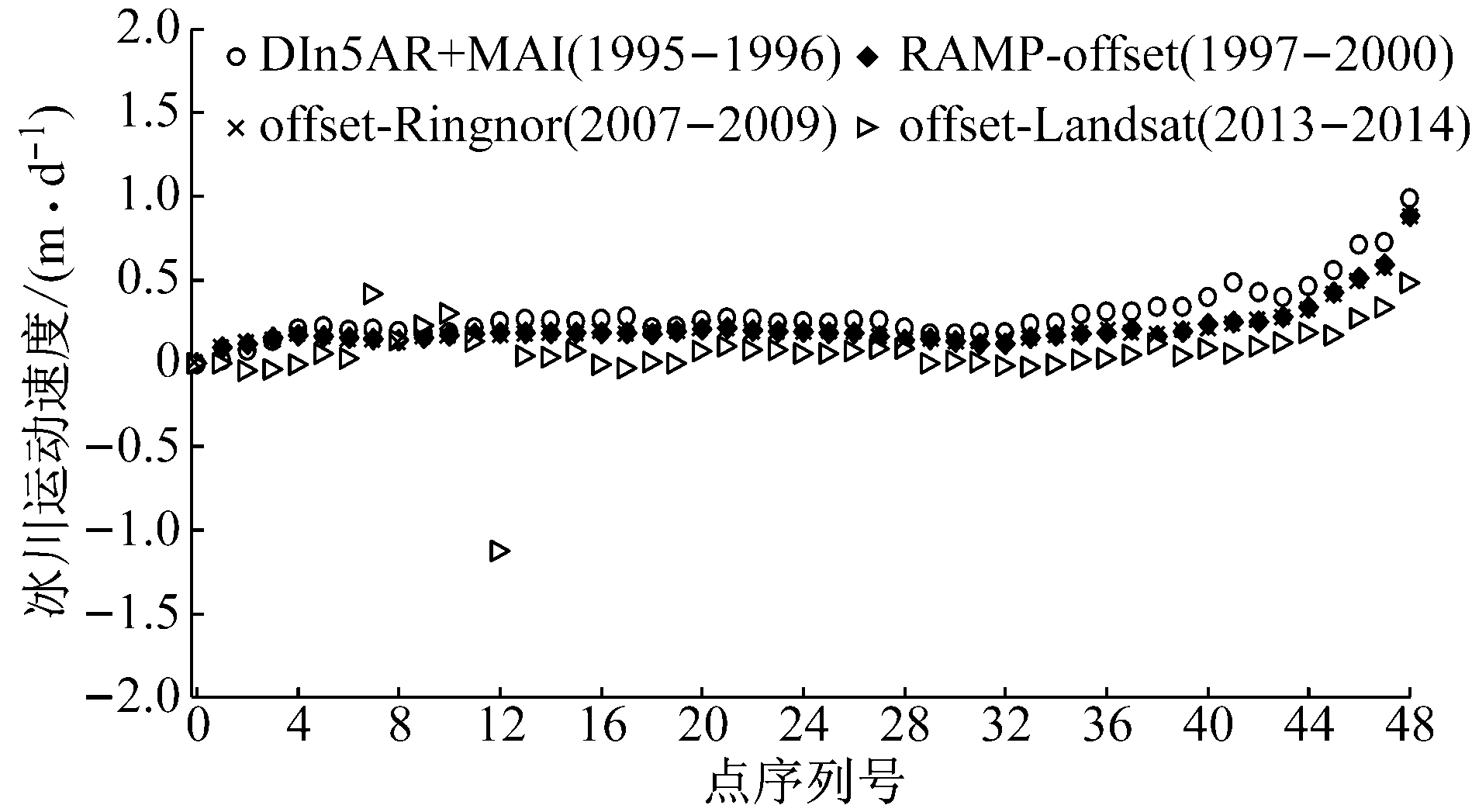
b Fisher冰川方位向冰川运动速度
图8 Fisher冰川运动速度对比分析
Fig.8 Ice flow velocity along the profile ofFisher Glaciers
4 结论
本文基于DInSAR和MAI技术在冰川运动速度提取中的优越性,提出了利用DInSAR和MAI方法的冰川运动速度提取算法,并将该算法应用于Lambert流域冰川运动速度的提取和冰川运动的时间序列特征分析.研究结果表明:
(1) DInSAR和MAI可以相互补充,能够应用于二维冰川运动速度场的提取,其中DInSAR提取的距离向冰川运动速度的精度为0.10 m·d-1; MAI提取的方位向的冰川运动速度的精度为0.07 m·d-1,优于传统的偏移量跟踪算法获取的冰川运动速度.
(2) 通过对Landsat 8数据采用偏移量跟踪算法获取的冰川运动速度及研究区域已有的研究成果进行对比,对Lambert流域冰川的运动特征及响应进行分析.研究结果表明,在过去的20年间,Lambert流域的冰川运动速度基本保持稳定,但是Lambert冰川具有轻微的加速,而Mellor冰川与Fisher冰川有轻微的减速.
参考文献:
[1] 王清华, 宁津生, 任贾文,等. 东南极Amery冰架与陆地冰分界线的重新划定及验证[J]. 武汉大学学报(信息科学版), 2002, 27(6): 591.
WANG Qinghua, NING Jinsheng, REN Jiawen, et al. Re-definition and validation of the grounding line of Amery ice shelf,East Antarctica [J]. Geomatics and Information Science of Wuhan University, 2002, 27(6): 591.
[2] 温家洪, JEZEK K C, CSATH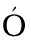 B M,等. 南极Lambert, Mellor和Fisher冰川的物质平衡及Amery冰架底部物质通量的估算[J]. 中国科学D辑(地球科学), 2007, 37(9): 1192.
B M,等. 南极Lambert, Mellor和Fisher冰川的物质平衡及Amery冰架底部物质通量的估算[J]. 中国科学D辑(地球科学), 2007, 37(9): 1192.
WEN Jiahong, JEZEK K C, CSATHó B M, et al. Mass budgets of the Lambert, Mellor and Fisher Glaciers and basal fluxes beneath their flowbands on Amery Ice Shelf [J]. Science in China Series D (Earth Sciences), 2007, 37(9): 1192.
[3] FRICKER H A, WARNER R C, ALLISON I. Mass balance of the Lambert Glacier—Amery Ice Shelf system, East Antarctica: a comparison of computed balance fluxes and measured fluxes[J]. Journal of Glaciology, 2000, 46(155): 561.
[4] JOUGHIN I, SMITH B E, ABDALATI W. Glaciological advances made with interferometric synthetic aperture radar [J]. Journal of Glaciology, 2010, 56(200): 1026.
[5] HANNA E, NAVARRO F J, PATTYN F, et al. Ice-sheet mass balance and climate change [J]. Nature, 2013, 498(7452): 51.
[6] 张小红, 鄂栋臣. 用PPP技术确定南极Amery冰架的三维运动速度[J]. 武汉大学学报(信息科学版), 2005, 30(10): 909.
ZHANG Xiaohong, E Dongchen. Dynamic parameters determination of Amery Ice Shelf using PPP [J]. Geomatics and Information Science of Wuhan University, 2005, 30(10): 909.
[7] 艾松涛, 王泽民, 鄂栋臣,等. 利用GPS的北极冰川运动监测与分析[J]. 武汉大学学报(信息科学版), 2012, 37(11): 1337.
AI Songtao, WANG Zemin, E Dongcheng, et al. Surface movement research of arctic glaciers using GPS method [J]. Geomatics and Information Science of Wuhan University, 2012, 37(11): 1337.
[8] 陈军, 柯长青. 南极冰盖表面冰流速研究综述[J]. 极地研究, 2015, 27(1): 115.
CHEN Jun, KE Changqing. Research progress on ice velocity of Antarctic ice sheet [J]. Chinese Journal of Polar Research, 2015, 27(1): 115.
[9] FREZZOTTI M, CAPRA A, VITTUARI L. Comparison between glacier ice velocities inferred from GPS and sequential satellite images [J]. Annals of Glaciology, 1998, 27: 54.
[10] MANSON R, COLEMAN R, MORGAN P, et al. Ice velocities of the Lambert Glacier from static GPS observations [J]. Earth Planets and Space, 2000, 52(11): 1031.
[11] ZHANG S K, E D C, WANG Z M. Ice velocities on the front of Amery Ice Shelf, East Antarctica, from static GPS observations[C]∥Geoinformatics 2006: GNSS and Integrated Geospatial Applications. [S.l.]: The International Society for Optical Engineering, 2006: 64180Q.
[12] QUINCEY D J, LUCKMAN A. Progress in satellite remote sensing of ice sheets [J]. Progress in Physical Geography, 2009, 33(4): 547.
[13] ROTT H. Advances in interferometric synthetic aperture radar (InSAR) in earth system science [J]. Progress in Physical Geography, 2009, 33(6): 769.
[14] 周春霞, 邓方慧, 陈一鸣,等. 利用SAR数据研究南极Grove山地区冰流运动特征[J]. 武汉大学学报(信息科学版), 2015,40 (11): 1428.
ZHOU Chunxia, DENG Fanghui, CHEN Yiming, et al. Ice-flow features in the Grove mountains area using SAR Data [J]. Geomatics and Information Science of Wuhan University, 2015, 40 (11): 1428.
[15] 李佳, 李志伟, 汪长城,等. SAR偏移量跟踪技术估计天山南依内里切克冰川运动[J]. 地球物理学报, 2013, 56(4): 1226.
LI Jia, LI Zhiwei, WANG Changcheng, et al. Using SAR offset-tracking approach to estimate surface motion of the south Inylchek glacier in Tianshan [J]. Chinese Journal of Geophysics, 2013, 56(4): 1226.
[16] BECHOR N B D, ZEBKER H A. Measuring two-dimensional movements using a single InSAR pair [J]. Geophysical Research Letters, 2006, 33(16):275.
[17] HU J, LI Z W, DING X L, et al. Resolving three-dimensional surface displacements from InSAR measurements: a review [J]. Earth-Science Reviews, 2014, 133(133): 1.
[18] JUNG H S, LU Z, WON J S, et al. Mapping three-dimensional surface deformation by combining multiple-aperture interferometry and conventional interferometry: application to the June 2007 eruption of Kilauea volcano, Hawaii[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(1): 34.
[19] BAMBER J L, GOMEZ-DANs J L, GRIGGS J A. A new 1 km digital elevation model of the Antarctic derived from combined satellite radar and laser data. Part 1: data and methods[J]. Cryosphere,2009,3, 101.
[20] COSTANTINI M. A novel phase unwrapping method based on network programming [J]. Geoscience and Remote Sensing, IEEE Transactions on, 1998, 36(3): 813.
[21] JEZEK K C. RADARSAT-1 Antarctic mapping project: change-detection and surface velocity campaign [J]. Annals of Glaciology, 2002, 34(1): 263.
[22] MOUGINOT J, SCHEUCHL B, RIGNOT E. Mapping of ice motion in Antarctica using synthetic-aperture radar data [J]. Remote Sensing, 2012, 4(12): 2753.
[23] RIGNOT E, MOUGINOT J, SCHEUCHL B. Ice flow of the Antarctic ice sheet [J]. Science, 2011, 333(6048): 1427.
Estimation and Evaluation of Ice Surface Velocity of Lambert Drainage of East Antarctica by Using Multi-Source Remote Sensing Datasets
Abstract: Ice surface velocity is one of the essential parameters for evaluating the mass balance and numerical simulation. In this paper, the research is mainly focused on the estimation of the ice surface velocity by combining the differential interferometry method and the multi-aperture interferometry method. The two-dimensional ice surface velocity of Lambert Drainage was estimated by employing the proposed method. A comparison between the estimated ice surface velocity and those obtained by using the offset tracking method and historical products was performed to analyze the dynamic characters. The results show that the proposed method is superior to the offset tracking method, and the glaciers in Lambert drainage is stable during the past 20 years.
Key words: ice flow velocity;differential interferometric synthetic aperture radar;multiple aperture interferometry; Lambert Glaciers; accuracy evaluation
收稿日期: 2017-04-21
基金项目: 国家“九七三”重点基础研究发展计划(2012CB957701);国家杰出青年科学基金(41325005)
中图分类号: TP751.1
文献标志码: A
